Психосемантическая феноменологическая модель групповой политической напряженности
Аннотация
Предложена модель групповой политической напряженности, выполненная в рамках теории катастроф. В качестве параметра порядка (ПП) используется обобщенная вероятность принятия или отрицания политического порядка. Роль управляющих параметров играют факторы эмоционального восприятия существующего политического порядка – сила, активность и оценка, впервые введенные Ч. Осгудом на основе метода семантического дифференциала. Определен типичный потенциал политической напряженности, градиент которого задает скорость изменения ПП, а на его основе – уравнение стационарных состояний. Проведена классификация типов решений этого уравнения. Получено, что при изменении внешних условий уровень политической напряженности может изменяться как непрерывно, так и скачком. Определены границы областей таких скачкообразных изменений (границы устойчивости различных типов решений уравнения состояния). Разработанная модель предназначена для оценки и прогнозирования уровня политической напряженности при экспериментальном анализе методов семантического дифференциала.
Ключевые слова: уровень, политическая напряженность, поведенческий компонент, аффективный компонент, теория катастроф, градиентная система, типичный потенциал, уравнения состояния, поверхности, типы решений, области устойчивости. № гос. регистрации 0421000096\00605.13.01 - Системный анализ, управление и обработка информации (по отраслям)
СКНЦ ВШ ЮФУ
В любом слое общества всегда есть какой-то уровень скрытой политической напряженности – «деформирующегося состояния социально-политического пространства без наблюдаемых признаков проекции напряжения на общественно-политическую ситуацию» [1]. Низкий уровень политической напряженности формирует политическое недовольство, а при дальнейшем увеличении ведет к политическому отчуждению. Высокий – является благодатной почвой для различного рода социально-политических протестов, от конвенциальных до неконвенциальных. Анализ и прогнозирование политической напряженности представляют большой интерес как с теоретической точки зрения, для понимания политических процессов, протекающих в обществе, так и с практической, для раннего предупреждения проекции напряженности на социальную ситуацию.
Феномен политической напряженности имеет системный, многогранный характер, определяется сложной сетью взаимодействия переменных, генерирующей системные свойства. Природа этого явления до конца не понята и в настоящий момент в научной литературе существует несколько подходов к этой проблеме. Депривационный подход [1-6], теория мобилизации ресурсов [7], «политическое» направление исследований [8] и др. Не отвергая результатов ни одного из этих подходов, отметим, что их многообразие связано с многогранностью исследуемого феномена, они отражают ту или иную его сторону. Выбор адекватного направления зависит, в частности, от поставленных задач и от исследуемых социальных групп. Для описания политической напряженности в Южном регионе, по нашему мнению, наиболее адекватно отражает ситуацию депривационный подход, и именно он положен в основу работы.
В соответствии с этим подходом непосредственными причинами формирования политической напряженности являются групповая относительная депривация и высокий потенциал социальной дифференциальной организации [1].
Теория относительной депривации была выдвинута в 50-х годах прошлого века [9] и исходит из идеи о том, что люди поддерживают политический порядок настолько, насколько он позволяет достигать им своих устремлений. Напряженность возникает тогда, когда группа начинает усматривать разрыв между своими устремлениями и доступными средствами [1].
Под относительной депривацией понимается «расхождение между субъективными ожиданиями определенных групп местного сообщества относительно материальных ресурсов и социальных статусов и их реальными возможностями получить доступ к этим ресурсам и статусам» [1].
Концепция «социальной дифференциальной организации» предложена Э.Сазерлендом для объяснения криминального девиантного поведения [10]. Его идея основана на том, что человек приобретает склонность к преступному поведению, если социализируется в группе, для которой подобное поведение является нормой. Согласно концепции, различные виды отклоняющегося поведения (в том числе и в политической сфере) распространяются вследствие такой организации локального сообщества, которая поддерживает установки индивидов на нарушение норм и ценностей социального прядка, в противовес установкам, не благоприятствующим нарушению таких норм.
Относительная депривация и потенциал социальной дифференциальной организации сами по себе также имеют системный характер и определяются объективными факторами (экономическими, социальными, религиозными, историческими и т.д.). Таким образом, схему формирования политической напряженности можно представить следующей диаграммой (см. рис. 1). Под влиянием объективных причин, существующих в обществе, формируется относительная депривация и социальная дифференциальная организация. Последние обуславливают групповую установку по отношению к существующему политическому порядку. Групповая установка состоит (как и любая установка по отношения к любому объекту или процессу) из трех компонент. Поведенческого (что делаю или буду делать), когнитивного (что знаю) и аффекивного (что чувствую).
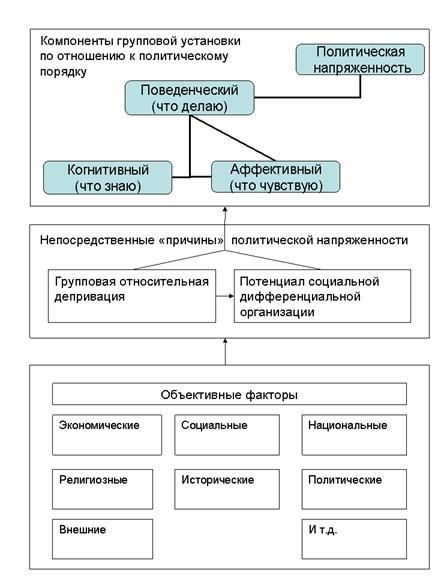
Рис. 1 Схема формирования политической напряженности
Политическая напряженность естественно связана с поведенческим компонентом групповой установки по отношению к существующему политическому порядку. И модель политической напряженности должна описывать связь поведенческого компонента с другими элементами диаграммы. Моделирование при этом может быть проведено для различных уровней. Целью настоящей работы является разработка модели для верхнего уровня – уровня групповой установки по отношению к существующему политическому порядку.
В качестве количественной меры политической напряженности в модели используется обобщенная вероятность поддержки или отрицания существующего политического порядка (r). Эта величина нормирована от -1 (полное неприятие политического порядка) до +1 (полное приятие). В модели она играет роль параметра порядка (ПП). Как показано в социальной психологии, поведенческий компонент групповой (и индивидуальной) установки по отношению к любому объекту связан с аффективным компонентом более существенно чем с когнитивным. Таким образом, в первом приближении можно считать, что введенная обобщенная вероятность определяется эмоциональным компонентом групповой установки по отношению к политическому порядку. И наша исследовательская задача – найти метод адекватного выявления эмоциональной (аффективной) составляющей установки и описать ее влияние на поведенческую составляющую. Для решения такой задачи разработаны «проективные методики», в частности метод семантического дифференциала. Последний предложен в 1952 г. Ч. Осгудом [11].
Метод семантического дифференциала является опросным. Респондентам предлагается оценить объект или процесс по биполярным шкалам, содержащим в качестве полюсов прилагательные-антонимы, которые описывают простейшие, первичные формы восприятия и эмоций: "холодный - теплый", "тупой - острый" и т.д. Предполагается, что человек способен оценить изучаемый объект, соотнося интенсивность внутреннего переживания с заданной оценочной шкалой [12]. Проведенные Осгудом и его многочисленными последователями исследования эмоциональных индивидуальных и групповых установок выявили следующий факт. Применяя факторный анализ к матрицам данных для разных респондентов, предлагая им для оценок разные объекты, используя разные шкалы, Осгуд получал один и тот же результат. Вся совокупность шкал как бы распадалась на три основные группы, на три независимых фактора. Он назвал их силой (за этим фактором стояли такие шкалы, как "сильный-слабый", "большой-маленький"), активностью ("активный-пассивный", "быстрый-медленный" и т.д.) и оценкой ("красивый-некрасивый", "хороший-плохой" и т.д.),. Иногда выделялись и другие факторы. Но на первом месте всегда стояли сила, активность и оценка. Этот феномен был назван Ч. Осгудом синэстезией. Универсальность полученных факторов по отношению и к объектам измерения, и к респондентам объясняется универсальностью, общностью для всех людей эмоционального кода [12].
Таким образом, поведенческий компонент групповой установки по отношению к политическому порядку, а вместе с ним и обобщенная вероятность поддержки или отрицания существующего политического порядка определяются тремя аффективными факторами – силы, активности и оценки. Следует подчеркнуть, что эти факторы характеризуют не сам политический порядок, а эмоциональное групповое отношение к нему. Фактор силы характеризует силу, интенсивность эмоционального восприятия политического порядка. Фактор активности – активность такого восприятия, а фактор оценки – эмоциональную оценку.
Социально-политические процессы, происходящие в обществе, индуцируют изменение групповой установки (и всех ее компонент) по отношению к политическому режиму. При этом в силу вышесказанного скорость изменения обобщенной вероятности поддержки или отрицания существующего политического порядка (dr/dt) зависит от аффективных факторов силы (d), активности (c) и оценки (b):
dr/dt = f(d, c, b). (1)
Групповое эмоциональное восприятия носит достаточно инерционный, гладкий характер и можно считать, что функция f в уравнении (1) непрерывна вместе со своими производными. В таком случае ее всегда можно представить как градиент некоторой другой функции F
dr/dt = - grad F. (2)
В работе рассмотрена квазистационарная ситуация, когда объективные условия меняются настолько медленно, что в каждый момент времени можно считать ситуацию статической. Тогда устойчивые значения ПП r определяется минимумом введенной функции F , которую можно назвать потенциалом политической напряженности.
Отметим, что этот потенциал мы ввели формальным, чисто математическим образом. Исходя из одномерности ПП и уравнения (1), гладкости функции f и условий устойчивости стационарного состояния. Однако использование потенциала политической напряженности в модели можно обосновать и исходя из социологических соображений. В социологии и политологии в конце прошлого века сформировалась теория «ожидаемой полезности» [13, 14], исходящая из максимизации «ожидаемой полезности» по параметрам, играющим роль акторов, при моделировании различных социально-политических процессов. Такие модели часто применяются в политической практике в качестве прескриптивных моделей (помогающие решить, какие меры следует принять) [13]. , На наш взгляд, их можно использовать и в дескриптивном моделировании (предсказывающем, что люди будут делать на самом деле), однако ожидаемая полезность в этом случае должна зависеть от аффективных составляющих групповых установок, так как именно они определяют поведенческий компонент. В частности, вводимый нами потенциал политической напряженности можно интерпретировать как одну из разновидностей «ожидаемой полезности» (взятую конечно с обратным знаком).
Таким образом, наша модель является градиентной динамической системой, роль параметра порядка играет обобщенная вероятность поддержки или отрицания существующего политического порядка (r), а поведение ПП описывается градиентом потенциала политической напряженности (уравнение 2), зависящим от трех управляющих параметров (d, b, c) – факторов сила, активность и оценка.
В теории катастроф [15] исследуются градиентные динамические системы общего положения. Под системами общего положения понимаются типичные и структурно устойчивые системы. Типичная система характеризуются следующим свойством: если мы в пространстве динамических систем с заданным числом управляющих параметров возьмем любую систему, то либо она окажется типичной, либо в любой ее бесконечной близости есть типичная система. Структурная устойчивость системы означает, что если мы немного (в теории – бесконечно мало) изменим параметры системы (не трогая число управляющих параметров), то свойства системы также изменятся бесконечно мало. Другими словами, система общего положения – это наиболее общая, ничем не выделенная система из класса всех систем с заданным числом управляющих параметров. Любую систему из этого класса мы можем превратить в систему общего положения малым шевелением параметров системы. В любом исследовании присутствует фактор стохастичности и фактор случайной ошибки. С учетом этого в естествознании принята концепция, что реально наблюдаются только типичные системы и только их следует изучать. В политологии и социологии фактор случайности играет еще большую роль, и следует ожидать, что и здесь эта концепция справедлива. В частности, используемые нами параметр порядка и управляющие параметры по своей природе стохастичны, и уравнения (1, 2) верны лишь в среднем и с какой-то точностью. Поэтому мы предположили, что наша градиентная динамическая система является типичной системой, системой общего положения.
В таком случае мы можем воспользоваться результатами теории катастроф [15], где доказано, что для динамических систем общего положения вид потенциала зависит только от числа управляющих параметров. И с точностью до гладкой замены переменных можно однозначно определить тип потенциала, Таким образом, если нам известен ПП и число управляющих параметров, то мы уже знаем конкретный вид потенциала и можем по нему провести исследование поведения системы (определить линии потери устойчивости и смены типа стационарных состояний). Поведение нашей конкретной системы может слегка отличаться от найденного, но топология поведения (то есть топология областей с различными видами состояний и линии смены типы состояния и потери устойчивости) не изменится.
Для рассматриваемого случая (одномерный ПП r и три управляющих параметра d, c, b) потенциал F определяется типичным сечением (в пространстве параметров управления) четырехпараметричной функции вида:
F=r6/6+ar4/4+br3/3+cr2/2+dr. (3)
В качестве такого сечения можно взять сечение, образованное линейной зависимостью параметра a от d, c, b.
Таким образом, в качестве потенциала политической напряженности можно взять функцию (3), для которой уравнение состояния, определяющее равновесное значение обобщенной вероятности r сводится к следующему
r5+ar3+br2+cr+d = 0. (4)
Где параметр a является линейной функцией от d, c, b.
Определение потенциала и расчет уравнений состояния были главными задачами при разработке нашей модели. Коэффициенты в (3) и (4) являются феноменологическими и определяются на основе экспериментальных данных. После их нахождения возможно рассчитать для конкретных ситуаций как стационарные значения обобщенной вероятности поддержки или отрицания существующего политического порядка так и ее динамическое поведение. Кроме того, полученные результаты позволяют выполнить классификацию возможных типов стационарных состояний.
В зависимости от величины фиксированных управляющих параметров (факторов сила, активность и оценка) потенциал политической напряженности может иметь: один минимум; два минимума и один максимум; три минимума и два максимума. Этому соответствует одно устойчивое стационарное состояние, два устойчивых и одно неустойчивое стационарных состояний и три устойчивых и два неустойчивых стационарных состояний соответственно. Все пространство управляющих параметров можно разделить гиперповерхностями потери устойчивости различных типов стационарных состояний на отдельные области. Внутри каждой области будет реализовываться свой тип решение уравнения состояния. Гиперповерхности потери устойчивости определяются из уравнения:
5r5+3ar2+2br+c = 0. (5)
Где значение параметры порядка необходимо брать из уравнения (4).
На рис. 2, взятом из [15], приведены проекции поверхностей потери устойчивости на плоскость d-c (факторы сила и активность) для различных фиксированных значений параметров a и b.
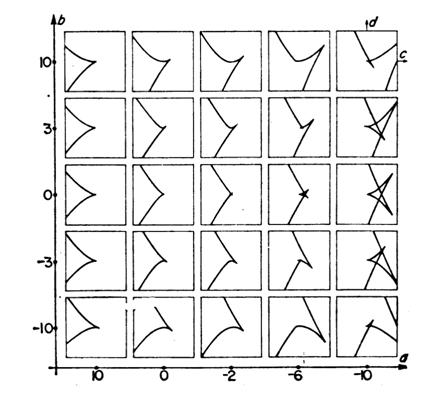
Рис. 2. Проекции поверхностей потери устойчивости.
Эти рисунки демонстрируют, как перестраиваются поверхности устойчивости при изменении внешних факторов. Для первых трех столбцов на всех рисунках, а для четвертого столбца – на нижнем и верхнем рисунках линия устойчивости не имеет самопересечения и образует «клюв». При значении параметров d и c вне «клюва» потенциал (3) имеет один минимум, а уравнение состояния (4) - одно решение. Для области внутри «клюва» потенциал политической напряженности имеет два минимума и один максимум, он описывает два устойчивых стационарных состояния и одно неустойчивое. На рис. 3a (весь рис. 3 также взят из [15]) над плоскостью d-c показана поверхность стационарных состояний для этого типа решений. Каждая точка этой поверхности образована стационарным значениями обобщенной вероятности, полученным из (4) для соответствующих значений d и c. В области перегиба этой поверхности нижний и верхний листы соответствуют устойчивым решениям, а средний – неустойчивому.
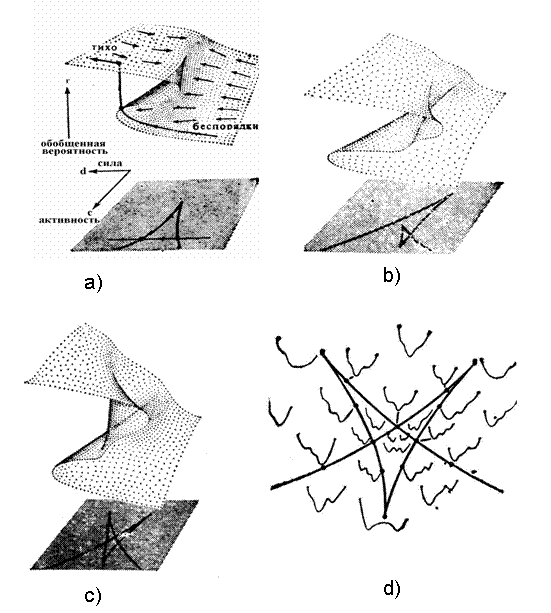
Рис. 3 Поверхности стационарных состояний (a, b и c). Перестройка потенциала политической напряженности(d).
При изменении внешних условий и параметров управления, точка стационарных решений перемещается по некоторой траектории на поверхности, при этом вне «клюва» обобщенная вероятность (и политическая напряженность) изменяются непрерывно. А в внутри «клюва», в области трех решений, медленное изменение внешних условий может привести к скачку политической напряженности (точка перескакивает с нижнего листа на верхний, либо наоборот). На рис. 3a для примера показана одна из таких траекторий, приводящая к скачкообразному уменьшению политической напряженности. Поверхность, изображенная на рисунке является сборкой и такое глобальное поведение системы в теории катастроф называется катастрофой сборки [15].
Возвращаясь к Рис. 2, отметим, что остальные рисунки, кроме выше упомянутых, демонстрируют более сложное поведение системы. На средних рисунках третьего слева столбца показано, что линии устойчивости начинают самопересекаться, с образованием замкнутых областей. Для четвертого слева столбца эти области увеличиваются. Здесь снаружи «клюва» (или того, что из него получилось) по прежнему находится область с одним стационарным состоянием. Внутри клюва, но вне замкнутой области с самопересечениями, имеется два устойчивых и одно неустойчивое решение, как и в предыдущем случае. В замкнутой же области, ограниченной со всех сторон линией устойчивости, система характеризуется уже тремя устойчивыми и двумя неустойчивыми стационарными состояниями. Поверхность стационарных состояний для этого типа решений приведена на Рис. 3 b и с. Видно, что над каждой точкой плоскости d-c внутри клюва эта поверхность имеет три или пять (внутри вышеуказанных замкнутых областей). На Рис. 3d качественно показана перестройка потенциала политической напряженности в окрестности точек самопересечения линии устойчивости. Если при изменении внешних условий управляющие параметры проходят через такие области, то возможно уже не один, а два скачка политической напряженности. Отметим, что такой тип поведения системы в теории катастроф называется катастрофой ласточкин хвост [15].
Один из этапов разработки модели – ее верификация. Для этого обычно рассчитывают модель по экспериментальным данным и сравнивают полученные результаты с реальными. По литературным данным нам удалось найти социологическое исследование [15, 16], позволяющее в некоторой степени верифицировать нашу модель. Это социологическое исследование нарушений режима в тюрьме Гартри (США) в течение 1972 г., проведенное Зиманом, Холлом, Хэррисоном, Мэрриджем и Шеплэндом. В работе исследовался уровень беспорядков от внутритюремных факторов. Каждое нарушение режима шкалировалось по степени серьезности от 0 до 10 методом экспертного опроса. Число беспорядков и степень их серьезности служило мерой уровня волнений. По результатам предварительного статистического факторного анализа данных было получено, что все учтенные факторы, влияющие на уровень беспорядков, разбиваются на две независимых группы, на два фактора. Авторы назвали их напряженностью (чувство разочарования и безысходности, бедственное положение) и разобщенностью (взаимная отчужденность, отсутствие общения, разбиение на два лагеря). Все полученные данные хорошо описываются катастрофой сборки, с осью напряженности, нормальной к острию, и осью разобщенности, идущей вдоль острия (см. Рис. 4).
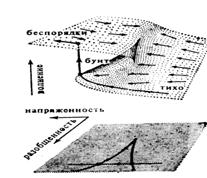
Рис. 4. Зависимость уровнябеспорядков от факторов напряженности и разобщенности.
На основе дальнейшего факторного анализа в качестве меры напряженности использовали сумму взвешенных значений еженедельного числа обращений к врачу, жалоб заключенных на недомогания во время работы, санкций, примененных начальником тюрьмы и благотворительных посещений. Мерой разобщенности являлась сумма числа заключенных, находящихся в карцере, и заключенных, просящих об отделении. Для выявления трендов результаты были сглажены. Проекция сглаженных результатов показана на Рис. 5.
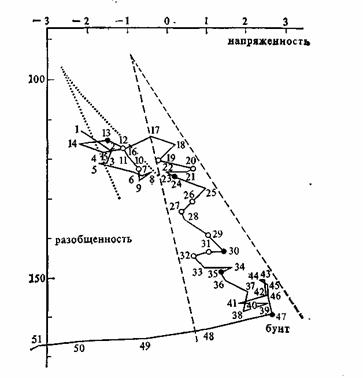
Рис. 5. Проекция сглаженных результатов на плоскость напряженность – разобщенность.
Здесь показано изменение во времени параметров управления, прослеженное неделя за неделей (номера недель приведены). Серьезные происшествия отмечены кружками. Для уточненных данных авторы выделяют не одну, а две катастрофы сборки, одну за первые 17 недель, и вторую за остальной промежуток времени. И связывают это с неучтенным фактором, который они назвали «лицо тюрьмы». В работе не исключается возможность, что это не две катастрофы сборки, а одна, с изогнутым «клювом», причем изгиб объясняют также влиянием третьего фактора.
Переходя к сопоставлению этого исследования с нашей моделью, отметим, что беспорядки в тюрьме и есть проявление социальной напряженности. И уровни этих двух величин пропорциональны. Факторы «напряженность» и «разобщенность» отражают в основном эмоциональное отношение заключенных к социальному порядку в тюрьме. Фактор «напряженность» характеризует силу, интенсивность эмоционального воприятия тюремного порядка, то есть близок к введенному Ч.Осгудом фактору сила. Переменная «разобщенность» определяется активностью аффективного восприятия этих порядком, то есть близка к фактору активность. Ну а параметр «лицо тюрьмы» полностью относится к эмоциональной оценке тюрьмы. Таким образом, и параметр порядка, и параметры управления в проведенном исследовании близки к аналогичным параметрам нашей модели. И результаты полностью качественно совпадают. На рис. 2 представлено несколько катастроф сборки с изогнутым клювом, одна из которых вполне может быть изображенной на Рис. 5.
В заключении кратко приведем полученные результаты.
-
Предложено в качестве параметра порядка, характеризующую политическую напряженность, использовать обобщенную вероятность поддержки или отрицания существующего политического порядка (r).
-
В этом случае поведение ПП полностью описывается потенциалом политической напряженности F, зависящем от трех аффективных факторов: силы (d), активности (c) и оценки (b) dr/dt = - grad F.
-
Определен типичный потенциал политической напряженности F=r6/6+ar4/4+br3/3+cr2/2+dr.
-
Равновесные состояния описываются минимумом этого потенциала, получено уравнение состояния и проведена классификация его решений.
-
В зависимости от величины факторов сила, активность и оценка может быть одно устойчивое стационарное состояние, два устойчивых и одно неустойчивое стационарных состояний и три устойчивых и два неустойчивых стационарное состояний.
-
При медленном (квазистационарном) изменении внешних условий политическая напряженность может изменяться как непрерывно, так и скачком. Найдены границы областей со скачкообразным изменением напряженности.
Литература
1. Э.Н. Ожиганов Политическая напряженность: имитационное моделирование и раннее предупреждение // Аналитический вестник Совета Федерации ФС РФ, 2008. № 9 (354).
2. Левада Ю. Массовый протест: потенциал и пределы // Экономические и социальные перемены: мониторинг общественного мнения. Информационный бюллетень, 1997. № 3. с. 7-12.
3. McAllister, I., White St. Political Participation in Postcommunist Russia: Voting, Activism, and the Potential for Mass Protest // Political Studies, 1994, XLII, pp. 593-615.
4. Davies J. C. Toward a Theory of Revolution // American Sociological Rev. 1962. 27 (February), pp. 5-19.
5. Gurr T. R. Why Men Rebel. Princeton, N.J.: Princeton University Press, 1970.
6. Feierabend, I. K., Feierabend R. L. Systemic conditions of political aggression: an application of frustration-aggression theory // Anger, Violence, and Politics. I. K. Feierabend, R. L. Feierabend, T. R.Gurr (eds.), Englewood Cliffs: Prentice-Hall, 1972, pp. 136-83.
7. Huntington S. P. Political order in Changing Societies. New Haven: Yale University Press, 1968.
8. В. В. Сафронов Потенциал протеста и демократическая перспектива // Журнал социологии и социальной антропологии, 1984, т.1, вып. 4.
9. Walker I., Smith H. (Eds.) «Relative Deprivation: Specification, Development and Integration”, Cambrige University Press, 2002
10. Ross L. Matsueda Differential Social Organization, Collective Action, and Crime// Crime, Law and Social Change Volume:46 Issue:1-2 , 2006, P. 3 – 33
11. Осгуд Ч., Суси Дж., Танненба-ум П. Приложение методики семантического дифференциала к исследованиям по эстетике и смежным проблемам // Семиотика и искус-ствометрия. М.: Мир, 1972
12. Т.С.Баранова Психосемантические методы в социологии //Социология: 4М. 1993-94. №3-4. С. 55-56
13. Э.Н. Ожиганов Моделирование и анализ политических процессов.- М., изд. РУДН, 2009, 189 С.
14. Bueno de Mesquite B., Lalman D. War and Reason: Domestic and International Imperatives.- New Haven: Yale University Press, 1992.
15. Т. Постон и И. Стюарт Теория катастроф и ее приложения.- М., Мир, 1980, 607 С.
16. E. C. Zeeman, C. Hall, P. J. Harrison, H. Marriage, P. Shapland A model for institutional disturbances. Br. J. Math. Statist. Psych. 29, 1976, P. 66—80.