Новые виды свай
Аннотация
Статья посвящена исследованию методик определения несущей способности винтовых и набивных свай. Представлены как аналитические подходы к решению согласно нормативным документам, так и численные с применением современных ЭВМ. Даны результаты численных экспериментов, выполненных в программном комплексе «Полюс».
Ключевые слова: винтовая свая, вдавливаемая свая, грунт, фундамент, несущая способность, метод конечных элементов, пластические деформации, гипотеза Кулона-Мора.
Устройство фундаментов, обладающих повышенной несущей способностью – одна из основных задач современного фундаментостроения. Свайные фундаменты в достаточной мере отвечают поставленным задачам. Однако строительство в условиях плотной городской застройки требует сохранности прилегающих к строящемуся сооружению уже существующих зданий. Таким образом, ограничена возможность применения забивных и вибровдавливаемых свай.
На сегодняшний день наиболее широко используются забивные, вибровдавливаемые и буровые сваи. Известным недостатком первых является их ограниченная применимость в плотной городской застройке. К недостаткам вторых так же можно отнести вибрационное воздействие и сложность монтажа. В случае же устройства третьих не происходит уплотнения грунта в околосвайной зоне. Близкими по технологии к буровым сваям являются усиления основания в виде армирующих элементов повышенной жесткости.
Эти проблемы послужили предпосылкой для разработки винтовых, обладающих повышенной несущей способностью. В 2010 году коллективом авторов разработаны и получены патенты на полезные модели винтовых свай (рег. № 98430, № 102631).
Предложенные ввинчиваемые сваи (монолитные и сборные) сочетают в себе лучшие качества забивных и буровых свай:
- при устройстве не будет оказываться динамическое воздействие на близлежащие объекты;
- в околосвайной зоне будет происходить уплотнение грунта и, как следствие, повышаться несущая способность.
- технология возведения менее требовательна к грунтовым условиям по сравнению, когда как технологически бывает невозможно произвести монтаж вибровдавливанием.
Оценка несущей способности ввинчиваемой сваи с учетом смятия околосвайного грунта и протекающих в этой зоне реологических процессов может быть выполнена посредством натурных испытаний, которые используют стандартную методику испытания свай согласно [1] и [2]. Упрощенно расчетная модель работы свай приводит к расширению известной формулы 7.11 (п. 7.2.6) [3].
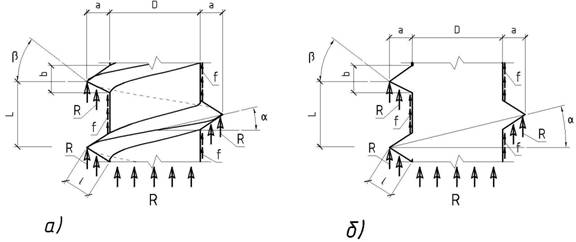
Рис. 1 Расчетные схемы в виде участка сваи конечной длины, где: а) схема ввинчиваемой ж/б сваи б) разрез ввинчиваемой ж/б сваи;
R – расчетное сопротивление под нижним концом сваи и нижней гранью резьбы, кПа
f – расчетные сопротивления на боковой поверхности ствола сваи, кПа
L – длина рассматриваемого участка, м
D – диаметр сваи, м
a – высота резьбы, м
b – ширина основания резьбы винта, м
α – угол подъема резьбы винта, град
β – угол профиля резьбы винта, град.
Согласно [1] отношение значений расчетных сопротивлений под нижним концом набивных и буровых свай (как и нижней гранью резьбы) и расчетных сопротивлений на боковой поверхности ствола сваи в условиях изменения Il=0,2 … 0,6 и глубины 3 … 20 м изменяются в 13,54 - 52,5 раз. Принимаем ![]() где k принимает значения от 13,5 до 52,5.
где k принимает значения от 13,5 до 52,5.
Для сравнительного анализа приняты следующие граничные условия и допущения:
- Расчетное сопротивление под нижним концом сваи и нижней гранью резьбы R – const;
- Расчетные сопротивления на боковой поверхности ствола сваи f - const;
- Диаметр сваи D – const;
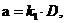 где
где 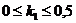 ;
;
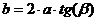 ;
;
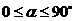 , при α=0 свая превращается в цилиндр диаметром
, при α=0 свая превращается в цилиндр диаметром 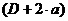 , при α=90° свая превращается в цилиндр диаметром D.
, при α=90° свая превращается в цилиндр диаметром D.
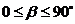 при β =0 сечение винта - становится прямоугольным, при β =90°- винт отсутствует.
при β =0 сечение винта - становится прямоугольным, при β =90°- винт отсутствует.
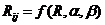 .
.
При этих допущениях несущая способность ввинчиваемой сваи при условии полного использования сопротивления под нижней гранью резьбы и отсутствия срыва будет равна: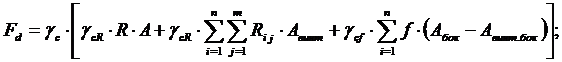
Где: ![]()
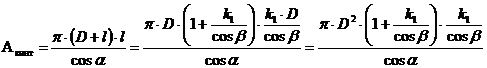 ,
,![]()
Уточнение работы сваи и грунтового массива можно получить путем использования современных методов строительной механики за счет модели, в которой нет априори введенной гипотезы кинематического либо статического характера. В данной работе использована пространственная расчетная модель «свая-массив грунта» в постановке осесимметричной деформации. При этом учитывался нелинейный характер работы грунта по гипотезе предельного равновесия (в первом приближении принята гипотеза Кулона-Мора). В дальнейшем планируется рассматривать так же критерий предельного состояния Мизеса-Шлейхера-Боткина.
В работе [5] были рассмотрены предельные нагрузки твердой среды, для которой объемное сжатие (растяжение) является упругой деформацией, изменяющейся согласно линейному закону. При сдвиге предполагалось, что материал подчиняется диаграмме Прандтля.
Таким образом, физические зависимости представляются в виде (1):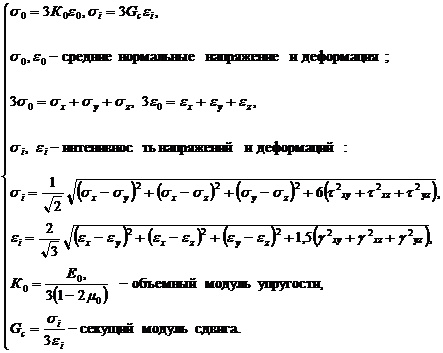 (1)
(1)
В соответствии с диаграммами деформирования, зависимости для модулей деформации имеют вид: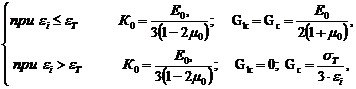 (2)
(2)
Согласно гипотезам (1) и с учетом обобщенного метода упругих перемещений линеаризованные физические зависимости принимают вид (3):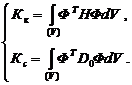 (3)
(3)
Решение упругопластической задачи проводим методом конечных элементов, линеаризация осуществляется шаговым методом. При использовании метода продолжения по параметру нагружения разрешающие уравнения для ансамбля конечных элементов записаны в (4).![]() (4)
(4)
При использовании простейших конечных элементов, в которых поле напряжений постоянно по объему элемента (треугольники) зоны пластичности последовательно возникают в объеме каждого конечного элемента, интенсивность напряжений которого достигла предела текучести. Для конечных элементов, в объеме которых поле деформаций изменяется по некоторому априори заданному закону, интегрирование при вычислении матриц жесткости выполняется численно. Поэтому здесь зоны пластичности последовательно возникают в группе расчетных точек (узлах интегрирования).
Алгоритм определения предельной нагрузки в континуальных системах, материал которых подчиняется условию текучести Губера-Мизеса следующий: на первом этапе формируется матрица жесткости для линейно-упругой среды и решается система уравнении МКЭ при "единичном" внешнем воздействии![]() , откуда
, откуда![]() .
.
По вектору узловых перемещений от "единичного" воздействия ![]() определяются во всех расчетных точках деформации и напряжения:
определяются во всех расчетных точках деформации и напряжения: ![]() . Параметр предельной нагрузки для каждой расчетной точки определяется из условия равенства интенсивности напряжений предельному значению, откуда σT:
. Параметр предельной нагрузки для каждой расчетной точки определяется из условия равенства интенсивности напряжений предельному значению, откуда σT: ![]() , откуда
, откуда ![]() . Здесь индекс r соответствует очередной расчетной точке области. Из множества значений параметров предельной нагрузки по всем точкам области выбирается наименьший
. Здесь индекс r соответствует очередной расчетной точке области. Из множества значений параметров предельной нагрузки по всем точкам области выбирается наименьший![]() , где е - общее количество расчетных точек.
, где е - общее количество расчетных точек.
На втором этапе учитываются зоны пластических деформаций, полученные после первого этапа. При формировании матриц жесткости в расчетных точках, в которых наступило предельное состояние, в соответствии с диаграммой деформирования ![]() .
.
Затем определяется приращение перемещений, деформаций и напряжений от единичной нагрузки: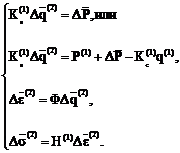 (5)
(5)
Приращения деформаций и напряжений линейны относительно параметра нагружения β, однако приращение интенсивности напряжений и деформаций является нелинейной функцией относительно β. Поэтому в каждой точке расчетной области для определения значения приращения нагрузки решается нелинейное относительно β уравнение (6) численным методом (в программном комплексе «ПОЛЮС» использован метод половинного деления с автоматическим выбором границ). Затем из множества значений β по всем расчетным точкам выбирается минимальное.
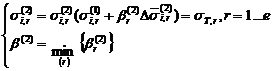 (6)
(6)
После определения параметра приращения нагрузки вычисляются приращения компонент и сами компоненты НДС в конце второго этапа (7).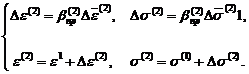 (7)
(7)
Итак, согласно критерию предельного состояния Мора - если оно достигнуто в состоянии преобладающего сжатия ( J1 < 0 ) , то дальнейшее поведение элементарного объема моделировалось при GK=0.
Рассмотрим модельный пример определения предельных нагрузок на винтовую сваю.
Грунтовые условия представлены одним ИГЭ со следующими физико-механическими характеристиками:
E=10 МПа, ν =0.35, с = 5 кПа, φ = 25º, γ=16 кН/м3.
Свая – бетонная, бетон класса В20, длиной 15 м.
Спектр нагрузок на сваю – от 100 кН до 450 кН с шагом в 50 кН.
Рассмотрен ряд расчетных схем:
- Свая винтовая – моделируется с зубьями в 2 этапа (на первом производится вдавливание сваи в грунт, а на втором – загружение сосной нагрузкой);
- Свая буровая – с диаметром равным диаметру тела сваи (0.3 м);
- Свая буровая – с диаметром равным диаметру тела сваи (0.4 м);
- Свая буровая – с диаметром равным диаметру тела сваи (0.5 м);
- Свая буровая – с диаметром равным диаметру тела сваи (0.6 м);
Полученные результаты показали значительное влияние на НДС системы процесса смятия околосвайного грунта. Задавливание проводилось поэтапно – по одной трети высоты сваи. Величина бокового перемещения составляла 5 см. Таким образом, моделировалось завинчивание сваи в лидерную скважину, диаметром 20 сантиметров. В результате деформирование от вертикальной нагрузки проходило не только непосредственно по телу сваи, но и в некотором объеме грунта. На рисунке 2 показаны зависимости вертикальной осадки свай от вертикальной нагрузки и диаметра свай.
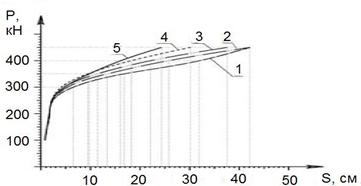
Рис.2 График зависимостей вертикальной осадки свай от вертикальной нагрузки и диаметра свай, где: 1 – график изменения осадки от вертикальной нагрузки для сваи диаметром 30 см, 2 – то же для сваи диаметром 40 см, 3 – то же для сваи диаметром 50 см, 4 – то же для сваи диаметром 60 см, 5 –то же для завинчиваемой сваи диаметром тела сваи 30 см и высотой резьбы – 15 см.
Литература:
1. СНиП 2.02.03-85. Свайные фундаменты. – Введ. 1987–01–01. – М.: Изд-во стандартов, 1987. – 54 с.: ил.; 29 см.
2. ГОСТ 5686-94. Грунты. Методы полевых испытаний сваями. – Введ. 1996–01–01. –М.: Изд-во стандартов, 1996. – 56 с.: ил.; 29 см.
3. СП 50-102-2003.Проектирование и устройство свайных фундаментов.– Введ. 2003–06–21. –М.: Изд-во стандартов, 2003. – 82 с.: ил.; 29 см.
4. ГОСТ 8732-78. Трубы стальные бесшовные горячедеформированные.– Введ. 1979–01–01. –
М.: Изд-во стандартов, 1979. – 11 с.
5. Панасюк Л.Н. Прямые методы решения нестационарных задач теории сооружений: дисс. … док. техн. наук: 05.23.17: – Рос