Алгоритм смешанного метода конечных элементов решения задач теории стержней
Аннотация
Дата поступления статьи: 05.11.2013Смешанный метод конечных элементов обладает преимуществами над классическими постановками данного метода в напряжениях и перемещениях и обеспечивает высокую точность и гладкость приближенных решений для силовых и кинематических неизвестных.
На практике, применение смешанного метода конечных элементов ограничено высокой размерностью получаемых систем сеточных уравнений, что приводит к существенному увеличению вычислительных затрат.
Применение ортогональных финитных функций для аппроксимации отыскиваемых величин приводит к формированию разреженных систем уравнений особой структуры, допускающей четырехкратное упрощение при их решении.
В статье предложен алгоритм модифицированного метода Гаусса для предварительного преобразования расширенной матрицы системы, на основе которого построен программный комплекс, включащий авторский решатель систем уравнений LISTSOLVER.
Подтверждена эффективность созданного решателя в сравнении с решателем общего типа.Ключевые слова: смешанный метод конечных элементов, разреженные системы линейных уравнений, ортогональные финитные функции, метод Гаусса
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Метод конечных элементов является эффективным инструментом решения краевыхзадач механики деформируемого твердого тела. Он может быть сформулирован в трех постановках (рис. 1).
Рис. 1. Виды формулировок метода конечных элементов
Методы в перемещениях и напряжениях, основанные на вариационных принципах Лагранжа и Кастильяно, обладают рядом недостатков, связанных с высокими требованиями к гладкости базисных функций, которые вызваны высоким порядком входящих вфункционал производных или необходимостью использования тензорныхполей напряжений, которые должны удовлетворять силовым краевым условиям и уравнениям равновесия.
Простота программной реализации и относительно высокая скорость получаемых решений обеспечили методам в перемещениях и напряжениях наибольшее распространение в конечно-элементных программных пакетах, таких как ANSYS.
Смешанный метод [1, 2]дает приближенные решения для перемещений и напряжений суравновешенной точностью и гладкостью в задачах теории стержней, пластин и оболочек,но, вместе с этим, имеет ряд недостатков, связанных с высокой размерностью получаемых систем сеточных уравнений, что приводит к существенному увеличению вычислительных затрат.
В работах [3, 4] были предложены способы устранения недостатков смешанных методов путем применения систем ортогональных финитных функций для аппроксимации отыскиваемых величин. Применение таких систем позволяет проводить исключение силовых неизвестных в аналитической форме до решения задачи на ЭВМ, что делает метод сравнимым по затратам машинного времени с методами, основанными на вариационных принципах Лагранжа и Кастильяно.
В работах[5, 6] приводятся примеры решения актуальных задач об изгибе балок. В работе [7] рассматривается тестовая задача об изгибе балки длиной ![]() , находящейся под действием распределенной поперечной нагрузки
, находящейся под действием распределенной поперечной нагрузки ![]() , жестко защемленной на левом конце и свободной на правом конце смешанным вариационно-сеточным методом. Для случая четырех отыскиваемых величин: перерезывающей силы
, жестко защемленной на левом конце и свободной на правом конце смешанным вариационно-сеточным методом. Для случая четырех отыскиваемых величин: перерезывающей силы![]() , изгибающего момента
, изгибающего момента ![]() , прогиба балки
, прогиба балки![]() и угла поворота сечения
и угла поворота сечения ![]() , применение ортогональных финитных функций в рамках такого метода приводит к локальной системе с глобальной матрицей, блоки которой, расположенные вдоль главной диагонали, имеют вид:
, применение ортогональных финитных функций в рамках такого метода приводит к локальной системе с глобальной матрицей, блоки которой, расположенные вдоль главной диагонали, имеют вид:

,
где ![]() — шаг равномерной сетки. Первая вспомогательная подчеркнутая строка не входит в состав матрицы и показывает соответствие столбцов блокаматрицы компонентам глобальной матрицы узловых неизвестных.
— шаг равномерной сетки. Первая вспомогательная подчеркнутая строка не входит в состав матрицы и показывает соответствие столбцов блокаматрицы компонентам глобальной матрицы узловых неизвестных.
При использовании трех узловых точексетки, делящих балку на две равных части, полная система уравнений для данной задачи в смешанной постановке с применением ортогональных финитных функций имеет вид:
 (1)
(1)
Обведенные числа соответствуют значениям коэффициентов при неизвестных на границах модели.
Особенностью системы уравнений (1) является возможность ее четырехкратного упрощения путем применения модифицированного метода Гаусса для предварительного преобразования расширенной матрицы. В общем виде алгоритм решения реализуется четырьмя последовательными этапами:
1. Прямой ход вдоль главной диагонали матрицы системы с исключением элементов, позиции которых кратны четырем (что соответствует столбцам и строкам для неизвестной W);
2. Формирование вторичной системы уравнений путем выделения из глобальной системы уравнений, соответствующих каждой четвертой строке, то есть W;
3. Решение вторичной системы, размерность которой в раз меньше размерности исходной системы, любым доступным методом [8, 9];
4. Подстановка найденных на предыдущем этапе узловых значений величиныW , в остальные уравнения исходной системы и решение этой системы с учетом свойств ортогональных финитных функций.
Рассмотрим расширенную матрицу системы (1):
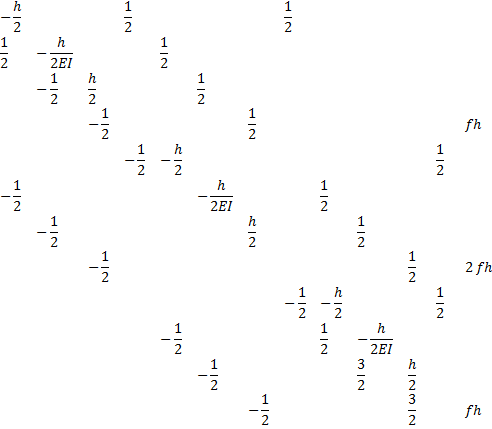
На первом шаге алгоритма элемент с индексами выбирается в качестве главного, все элементы первой строки делятся на него, при этом на позиции главного элемента возникает единица. Затем из каждой строки, кроме первой, содержащей в первом столбце ненулевое значение, производится вычитание первой строки, умноженной на это значение. Таким образом, в первом столбце остается только одно ненулевое значение:
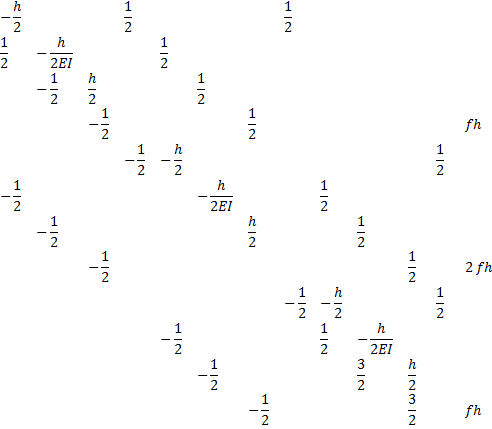
На втором и третьем шагах аналогичные операции проводятся после выбора в качестве главных следующих элементов с индексами ![]() и
и ![]() , , что приводит расширенную матрицу к виду:
, , что приводит расширенную матрицу к виду:
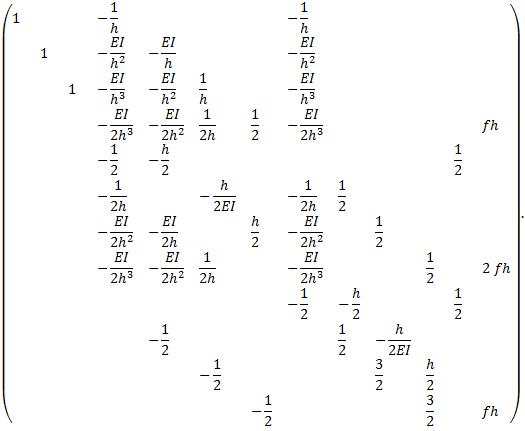
В результате, исключая обработку элементов главной диагонали с индексами 4, 8 и 12, исходная система уравнений (1) принимает вид:
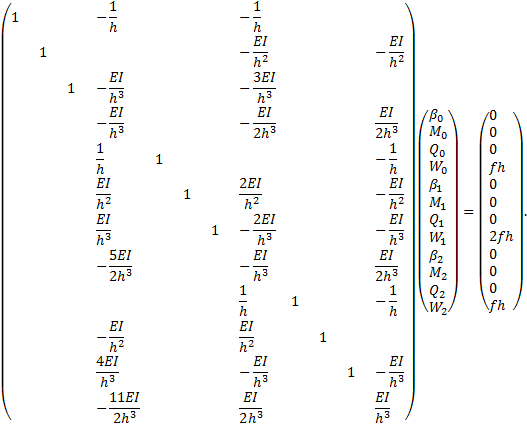 (2)
(2)Особенностью системы (2) является независимость отыскиваемых величин![]() , от остальных и наоборот — каждая из величин
, от остальных и наоборот — каждая из величин![]() ,
, ![]() и
и ![]() зависит только от
зависит только от![]() . Это позволяет выделить из данной системы подсистему меньшей размерности:
. Это позволяет выделить из данной системы подсистему меньшей размерности:
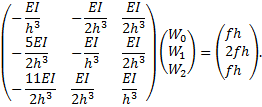
Решение подсистемы меньшей размерности может быть получено за значительно меньшее время. Полное решение системы уравнений (2) получается после подстановки найденных для величины![]() результатов в остальные уравнения, из которых без дополнительных преобразований сразу находятся узловые значения
результатов в остальные уравнения, из которых без дополнительных преобразований сразу находятся узловые значения ![]() ,
, ![]() и
и ![]() .
.
Для подтверждения эффективности предложенного алгоритма были разработаны программные модули решения систем уравнений UMFSOLVER (решает полную систему уравнений) и LISTSOLVER (реализует предложенный алгоритм)в рамках авторского программного комплекса конечно-элементного анализа в смешанной форме ViSolver.
Результаты сравнения времени решения задачи с помощью решателей программного комплекса представлены в таблице 1.
Таблица 1
Время решения задачи двумя типами решателей
Количество конечных элементов |
10 |
100 |
1000 |
10 000 |
100 000 |
|
Время решения в UMFSOLVER, сек. |
4,8e-04 |
2,6e-03 |
2,3e-02 |
2,3e-01 |
2,4 |
|
Время решения в LISTSOLVER, сек. |
3,5e-04 |
1,5e-03 |
1,4e-02 |
1,4e-01 |
1,4 |
|
Прирост производительности при использовании LISTSOLVER, % |
27 |
40 |
40 |
40 |
42 |
Важно отметить, что решение в программной среде UMFSOLVER проводилось для смешанного метода с использованием ортогональных функций путем решения полной системы вида (1), которая имеет заведомо меньшее количество ненулевых элементов, чем система для классических аппроксимирующих функций метода конечных элементов (функций Куранта). Сравнение, основанное на разнице в типах аппроксимирующих функций, было изложено в работе [10].
Полученныерезультаты позволяют сделать вывод об увеличении скорости решения, получаемого с помощью LISTSOLVER, более чем в 1,5 раза при сохранении высокой точности отыскиваемых величин.
Относительная простота и независимость преобразований над группами столбцов расширенной матрицы, принадлежащих соседним элементам, позволяют прийти к выводу о возможности распараллеливания алгоритма и его эффективного применения при расчетах в кластерных системах.
Таким образом, проведенное исследование позволило оценить эффективность модифицированного алгоритма решения систем линейных уравнений, полученных смешанным методом конечных элементов с использованием ортогональных финитных функций, и оценить возможности дальнейшего развития предложенного алгоритма и программного пакета на его основе.
Список литературы:
- Reissner E. On a variational theorem in elasticity // Journal of Mathematical Physics. — 1950. — Vol. 29. — №2. — PP. 90-95.
- Washizu K. Variational Methods in Elasticity and Plasticity. – Oxford: Pergamon Press, 1975. – 420 p. – ISBN 0-08-017653-4.
- Леонтьев В.Л. Ортогональные финитные функции и численные методы. – Ульяновск: Изд-во УлГУ, 2003. – 177 с. – ISBN5-88866-144-9.
- Леонтьев В.Л.Об ортогональных финитных функциях и связанных с ними вариационно-сеточных методах решения краевых задач// Труды Всероссийской научной конференции (26-28 мая 2004 г.). Часть 3. Дифференциальные уравнения и краевые задачи. Математическое моделирование и краевые задачи. – 2004. – С. 140-143.
- Бурцева О. А., Косенко Е.Е., Косенко В.В., Нефедов В.В., Черпаков А.В. Моделирование напряженного состояния арматурных стержней, применяемых при производстве преднапряженных железобетонных конструкций [Электронный ресурс] // «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2011/549 (доступ свободный) – Загл. с экрана. – Яз.рус.
- Лукин А.О. Определение прогибов балок с гофрированной стенкой с учетом сдвиговых деформаций [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2013/1496(доступ свободный) – Загл. с экрана. – Яз.рус.
- Лавыгин Д.С., Леонтьев В.Л. Смешанный вариационно-сеточный метод, связанный с ортогональными финитными функциями, в задачах теории стержней // Прикладная математика и механика: сборник научных трудов. – Ульяновск:УлГТУ, 2011. – 505 с. – ISBN 978-5-9795-0904-4.
- Gould N., Scott J. A. A numerical evaluation of sparse direct solvers for thesolution of large sparse symmetric linear systems of equations // ACM Transactions on Mathematical Software. –2007. –Vol. 33. – №2. –PP. 1-32. – ISSN 0098-3500.
- Davis T. A., Duff I. S. A combined unifrontal/multifrontal method forunsymmetric sparse matrices // ACM Transactionson Mathematical Software. – 1999. – Vol. 25. – №1. – PP. 1-20. – ISSN0098-3500.
- Лавыгин Д.С., Леонтьев В.Л. Смешанный метод конечных элементов, связанный с использованием ортогональных финитных функций // Математические методы и модели: теория, приложения и роль в образовании: сборник научных трудов. – Ульяновск:УлГТУ, 2011. – 311 с. – ISBN 978-5-9795-0905-1.