Выбор шага в задачах динамики пространственно-распределенных объектов на основании спектрального условия устойчивости
Аннотация
Моделированием пространственно-распределённых систем занимаются достаточно давно. С тех пор решены проблемы устойчивости разностных методов применительно к стандартным задачам математической физики. Подобные модели находят применение при решении задач прогнозирования погоды, расчёта температурных и магнитных полей, а также при построении систем управления сложными и распределёнными объектами. В настоящее время созданы компьютерные модели, основанные на классических уравнениях математической физики и теории сплошных сред. Для моделей технологических процессов, содержащих кроме указанных уравнений ещё и логические зависимости, общих методов генерации расчётной сетки не предложено. В данной статье будет описан алгоритм автоматической подстройки шага, учитывающий спектральное условие устойчивости для математических моделей, которые заданы уравнениями и алгоритмами. Это характерно для гибридных математических моделей. Рассмотрение таких моделей актуально с точки зрения современной теории управления. Ключевые слова: магистральный газопровод, моделирование, пространственная сетка, граничные условия
05.13.06 - Автоматизация и управление технологическими процессами и производствами (по отраслям)
ДГТУ
Введение. Моделированием пространственно-распределённых систем занимаются достаточно давно. С тех пор решены проблемы устойчивости разностных методов применительно к стандартным задачам математической физики. Подобные модели находят применение при решении задач прогнозирования погоды, расчёта температурных и магнитных полей, а также при построении систем управления сложными и распределёнными объектами. В настоящее время созданы компьютерные модели, основанные на классических уравнениях математической физики и теории сплошных сред. Для моделей технологических процессов, содержащих кроме указанных уравнений ещё и логические зависимости, общих методов генерации расчётной сетки не предложено. В данной статье будет описан алгоритм автоматической подстройки шага, учитывающий спектральное условие устойчивости для математических моделей, которые заданы уравнениями и алгоритмами. Это характерно для гибридных математических моделей. Рассмотрение таких моделей актуально с точки зрения современной теории управления.
Существо проблемы. При решении задачи интегрирования системы, которая описывает динамику пространственно распределённой системы (ПРС), когда схема пространственной аппроксимации уже найдена, появляется проблема выбора шага интегрирования по времени. Такая задача возникает при математическом моделировании протяжённых технологических объектов. Многие исследователи выбирают шаг, исходя из энергетических соображений или из требований точности и аппроксимации. Как правило, более жёстким ограничением на величину шага является спектральное условие устойчивости Неймана, которое гласит, что оператор перехода с одного временного слоя на другой должен иметь спектр, распределённый на отрезке [-1,1]. При интегрировании систем ДУ, описывающих динамику ПРС, можно рассчитать максимально допустимый шаг по условиям Куранта-Фридрихса-Леви (КФЛ); но при решении задач имитационного моделирования ПРС, величина шага, вычисленная по этим критериям, оказывается очень маленькой для того, чтобы решать эти задачи в реальном времени. В данной статье предлагается вариант алгоритма оперативной подстройки величины шага по времени на основании распределения спектра оператора временного перехода.
Математическая постановка задачи. Исследуемая система, как правило, описывается системой дифференциальных уравнений в частных производных (ДУЧП). Дискретизация исходной модели по пространственным координатам приводит к переходу от ДУЧП к системе уравнений в полных производных, описывающей эволюцию системы. Эту систему можно, как правило, представить в виде задачи Коши
![]() (1)
(1)
Процесс нахождения решения дискретной динамической системы (1) методом Эйлера описывается следующими итерационными формулами:
![]() , (2)
, (2)
где ![]() - сеточная функция, определяющее приближенное решение,
- сеточная функция, определяющее приближенное решение, ![]() - функция правой части системы дифференциальных уравнений,
- функция правой части системы дифференциальных уравнений, ![]() - независимая координата,
- независимая координата, ![]() - величина шага метода Эйлера. Обозначим Якобиан функции
- величина шага метода Эйлера. Обозначим Якобиан функции ![]() через
через ![]() ,
, ![]() .
.
Спектр оператора временного перехода в соответствии с методом Эйлера определяется по формуле ![]() , где
, где ![]() - оператор одного шага (шага вперёд) в дискретном времени,
- оператор одного шага (шага вперёд) в дискретном времени, ![]() – оператор тождественного преобразования,
– оператор тождественного преобразования, ![]() – линейный оператор, приближающий функцию
– линейный оператор, приближающий функцию ![]() .
.
Для задачи имитационного моделирования условие устойчивости означает, что погрешности и неточности, возникающие в результате действий над числами с плавающей точкой (при вычислении правых частей системы дифференциальных уравнений), приведут к затухающим переходным процессам по ошибке моделирования. Анализ уравнения (2) показал, что спектр дискретной системы (2) можно менять в широком диапазоне, варьируя величину ![]() . Так как устойчивость алгоритма определяется
. Так как устойчивость алгоритма определяется ![]() , то наложим на оператор
, то наложим на оператор ![]() ограничения, задающие условия устойчивости
ограничения, задающие условия устойчивости ![]() .
.
Описание алгоритма. Задача автоматической подстройки шага заключается в том, чтобы для устойчивых корней из спектра оператора ![]() подобрать такое значение
подобрать такое значение ![]() , при котором собственные значения оператора
, при котором собственные значения оператора ![]() будут проектироваться во внутренность единичной окружности. В математическом выражении:
будут проектироваться во внутренность единичной окружности. В математическом выражении: ![]() найти
найти ![]() , где
, где ![]() - спектр оператора
- спектр оператора ![]() , a
, a ![]() - спектр оператора
- спектр оператора ![]() .
.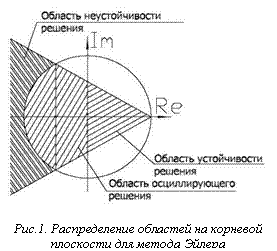 При изменении величины шага
При изменении величины шага ![]() собственные значения оператора
собственные значения оператора ![]() перемещаются внутри конуса (рис. 1). Величина угла в вершине конуса зависит от максимума отношения действительных и мнимых частей граничных собственных значений оператора
перемещаются внутри конуса (рис. 1). Величина угла в вершине конуса зависит от максимума отношения действительных и мнимых частей граничных собственных значений оператора ![]() . При достаточно маленьких
. При достаточно маленьких ![]() весь спектр оператора
весь спектр оператора ![]() распределён в области устойчивости решения (см. рис.1).
распределён в области устойчивости решения (см. рис.1).
При увеличении ![]() спектр оператора
спектр оператора ![]() смещается в отрицательную область (в область осциллирующего решения и в область неустойчивости). На основе анализа границ спектра можно определить, удовлетворяет ли величина
смещается в отрицательную область (в область осциллирующего решения и в область неустойчивости). На основе анализа границ спектра можно определить, удовлетворяет ли величина ![]() условиям устойчивости, и как надо изменить величину
условиям устойчивости, и как надо изменить величину ![]() для обеспечения устойчивости.
для обеспечения устойчивости.
Условия устойчивости и отсутствия осцилляции могут быть записаны (для метода Эйлера) в следующей форме:
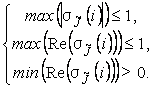 (3)
(3)
Для автоматической подстройки шага необходимо найти спектр оператора ![]() для текущей и для увеличенной (например, в два раза) величины шага -
для текущей и для увеличенной (например, в два раза) величины шага - ![]() и
и ![]() . Если оба спектра удовлетворяют условиям
. Если оба спектра удовлетворяют условиям ![]() - устойчивости и условиям отсутствия осцилляции (3), то величину текущего шага можно увеличить. Если спектр
- устойчивости и условиям отсутствия осцилляции (3), то величину текущего шага можно увеличить. Если спектр ![]() не удовлетворяет условиям (3), то величину шага изменять не следует. Если же оба спектра не удовлетворяют условию (3), то величину шага целесообразно уменьшить (рис. 1).
не удовлетворяет условиям (3), то величину шага изменять не следует. Если же оба спектра не удовлетворяют условию (3), то величину шага целесообразно уменьшить (рис. 1).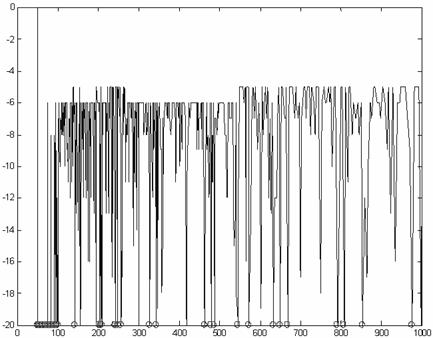
Рис.2. Зависимость величины логарифма (по основанию 2) шага от времени
Выводы
Этот алгоритм целесообразно применять, когда спектр оператора ![]() располагается достаточно компактно на комплексной плоскости. Однако, данный алгоритм нельзя использовать в случае жёстких систем дифференциальных уравнений, для которых характерен очень широкий спектр.
располагается достаточно компактно на комплексной плоскости. Однако, данный алгоритм нельзя использовать в случае жёстких систем дифференциальных уравнений, для которых характерен очень широкий спектр.
Экспериментально-вычислительный анализ (рис. 2) показал, что моделирование выбранным методом Эйлера протекает исключительно долго, потому что увеличение шага происходит только при переходе моделируемой системы (исследовалась математическая модель магистрального газопровода) в режим, близкий к стационарному. Предложенный подход, связанный с удвоением шага, может быть использован для реализации алгоритмов параллельного моделирования ПРС, когда модель распадается на несколько моделей, функционирующих с разной скоростью.
В настоящее время проводится проверка локальной адекватности исходной математической модели ПРС и её линеаризованного приближения, восстановленного по всем элементам спектра. Оно основывается на приближённом вычислении матрицы Якоби, смене базиса модели при переходе в жорданову нормальную форму (ЖНФ). В форме ЖНФ легко получить выражения, описывающие свободные движения динамической системы. В случае адекватности приближения на некотором временном интервале, можно рассчитывать, в силу жесткости исходной математической модели, на проведение процедуры автономизации жестких компонентов в базисе ЖНФ для распараллеливания процесса моделирования.
Для моделирования быстрых процессов нужен частый шаг и много итераций. Если процесс настолько быстрый, что ЭВМ, в реальном времени, не справляется с его воспроизведением, разумно перейти к вычислениям по неявной разностной схеме. Тогда шаги можно делать, исходя из доступных вычислительных ресурсов и ограничений на скорость моделирования.
Положительный результат подобных исследований зависит от свойств модели ПРС. Описанное распараллеливание приводит к уменьшению вычислительной сложности моделирования в жесткой задаче, когда количество быстрых компонентов решения меньше количества медленных компонентов. Большей эффективности можно достичь, исследовав и применив описанный подход к методам с большей областью устойчивости, нежели у метода Эйлера, например, к методам Рунге-Кутта или Адамса.
Список использованной литературы
- С.К. Годунов, В.С. Рябенький. Разностные схемы. – М.:Наука,1973.
- М.Ю. Белевич. Математическое моделирование гидрометеороло-гиических процессов. – СПб., 2000.
- А.Н. Минайлос. Дефект точности дифференциальных уравнений в численном решении. – М.: ЦАГИ, 2001.
- Самарский А.А. Введение в теорию разностных схем. – М.: Наука, 1971.
- А.Н. Тихонов, А.А. Самарский. Уравнения математической физики. Главная редакция физико-математической литературы изд-ва "Наука", 1966.
20 июня 2008 г.