Применение адаптивного модифицированного попеременно–треугольного итерационного метода для численной реализации двумерной математической модели движения водной среды

Аннотация

А.Е.Чистяков, Н.А.Фоменко

Модифицированный попеременно-треугольный метод вариационного типа применяется для численной реализации двумерной дискретной математической модели движения водной среды. Данная модель построена на основе трехмерной гидростатической модели. Исходными уравнениями, которой являются: уравнение для несжимаемой жидкости, уравнение гидростатики и система уравнений Навье-Стокса. Разработанная модель предназначена для прогнозирования процессов заиливания и воздействия негативных факторов, влияющих на состояние прибрежной зоны и береговых сооружений. В работе представлен алгоритм модифицированного попеременно – треугольного итерационного метода минимальных поправок для расчета сеточных уравнений Приведены результаты численных экспериментов.
Ключевые слова: Итерационные методы, гидродинамика, дискретная модель, сеточные уравнения, система уравнений Навье-Стокса.

Ключевые слова:

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Моделирование процессов происходящих в водной среде имеет значение не только при исследованиях водных экосистем, экологического состояния водоемов, параметров водной среды, но и при проектировании и возведении прибрежных сооружений, так как воздействия  волн и прибоя к берегам различных водоемов приводит к их разрушению. А так же непрерывное движение водной среды приводит к необратимым последствиям, таким как изменение рельефа дна. Последствия данных явления можно наблюдать на побережьях океанов, морей и крупных озер. Строительство берегозащитных сооружений, ограждающих дамб, волнорезов, волновых молов является дорогостоящим и технически сложным мероприятием. Поэтому моделирование данных процессов является важным не только для экологии, но и для экономики.
Для прогнозирования процессов заиленья, негативных факторов, влияющих на эксплуатацию прибрежной зоны и береговых сооружений необходимо детально исследовать гидродинамические процессы, происходящие в водной среде.
Для построения двумерной математической модели движения водной среды нам понадобится двумерная модель гидродинамики[1,2] исходными уравнениями которой являются:
– двумерный аналог системы уравнений Навье-Стокса

,

(1)

- аналог уравнения неразрывности для несжимаемой жидкости
.         (2)
где  – функция подъема уровня,  – вектор скорости движения водной среды,  – давление, – коэффициент турбулентного обмена по горизонтальному направлению,  – ускорение свободного падения,  – плотность жидкости, ,  – тангенциальное напряжение на дне и поверхности жидкости соответственно, – глубина водоема, отсчитываемая от невозмущенной водной поверхности.
Математическая модель (1)-(2) учитывает геометрию донной поверхности и функцию возвышения уровня. Данная система уравнений рассматривается при следующих граничных условиях:
.     (3)
Условие (3) описывает свободный выход на боковых границах.
Построение двумерной модели гидродинамики.
Расчетная область вписана в прямоугольник. Покроем область равномерной прямоугольной расчетной сеткой :

,

где  – индексы по временной координате и пространственным координатным направлениям,,  соответственно,  – шаги по временной координате и пространственным координатным направлениям,,  соответственно,  – количество узлов по временной координате и пространственным координатным направлениям , ,соответственно,  – длина расчетной области по временной координате и пространственным координатным направлениям ,  ,соответственно.
Дискретный аналог модели движения водной среды, представленной уравнениями (1)-(2), согласно методу поправки к давлению[3] запишется в виде следующей системы уравнений, в которой первое уравнение записывается без учета функции возвышения на первом временном слое:

,

(4)

С учетом выполнения (2),(3) аналога уравнения неразрывности для несжимаемой жидкости, данное уравнение можно представить в виде:

(5)
,
а затем на следующем временном слое:
,        (6)
.
Для построения конечно-разностных схем использован метод баланса.
Дискретные аналоги операторов конвективного  и диффузионного  переноса в случае частичной заполненности ячеек в случае граничных условий третьего рода:
,         
могут быть записаны в следующем виде [4]:
,


где ,  - коэффициенты, описывающие заполненность контрольных областей.
Полученные сеточные уравнения решались модифицированным попеременно-треугольным итерационным методом, алгоритм которого представлен ниже.
Адаптивный модифицированный попеременно-треугольный метод вариационного типа. Рассмотрим задачу об отыскании решения операторного уравнения в конечномерном гильбертовом пространстве H:
,      (10)
где A – линейный, положительно определенный оператор ( ).Для нахождения задачи (14) будем использовать неявный итерационный процесс
,       (11)
где m – номер итерации, τ> 0 –итерационный параметр, а B – некоторый обратимый оператор. Обращение оператора B в (11) должно быть существенно проще, чем непосредственное обращение исходного оператора Aв (10). При построении B будем исходить из аддитивного представления оператора - симметричной части оператора А
(12)
Также здесь и далее будем использовать кососимметричную часть оператора А
.
В силу (12) . Поэтому в (12) . Пусть в (11)

,     (13)
где – некоторый оператор.
Поскольку , то вместе с (12) это дает . Соотношения (11)-(13) задают модифицированный попеременно-треугольный метод (МПТМ) решения задачи[5-7], если определены операторы  и указаны способы определения параметров ,  и оператора .
Алгоритм модифицированного попеременно – треугольного итерационного метода минимальных поправок для расчета сеточных уравнений имеет вид
,  , ,
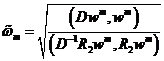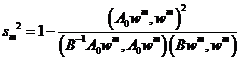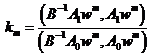, ,      (14)
, , , .
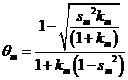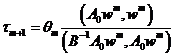В адаптивном попеременно - треугольном методе в качестве параметра используется значение с предыдущей итерации с этим и связан локальный рост нормы вектора невязки.

Рис.1.Зависимость нормы вектора невязки от количества итераций.

Из рис. 1 видно что, при решении сеточного уравнения адаптивным попеременно-треугольным методом равномерная норма вектора невязки (максимальный по модулю элемент) убывает достаточно быстро, но возможен локальный рост погрешности. В таблице 1 приведены результаты сравнения ПТМ и МВР.

Таблица 1.

Из приведенной таблицы видно, что выбор адаптивного модифицированного попеременно-треугольного метода вариационного типа является более предпочтительным по сравнению с методом верхней релаксации при решении сеточных уравнений, полученных в результате аппроксимации задач волновой гидродинамики.

Литература
1.Сухинов А.И., Чистяков А.Е., Проценко Е.А. Двумерная гидродинамическая модель, учитывающая динамическое перестроение геометрии дна мелководных водоемов. Известия ЮФУ. Технические науки. – Таганрог: Изд-во ТТИ ЮФУ, 2011, №8(121). С. 159-167.
2.Фоменко Н.А. Моделирование гидродинамических процессов  при обтекании корпуса судна. Известия ЮФУ. Технические науки. Тематический выпуск «Актуальные проблемы математического моделирования». – Таганрог: Изд-во ТТИ ЮФУ, 2011, №8(121). С.139-147.
3.Чистяков А.Е., Фоменко Н.А. Построение двумерной математической модели движения водной среды // Журнал ТТИ ЮФУ. Информатика, вычислительная техника и инженерное образование №5(7)-2011, Электронный журнал. С. 59-66.
4.Чистяков, А. Е. Об аппроксимации граничных условий трехмерной модели движения водной среды// Известия ЮФУ. Технические науки. Тематический выпуск «Актуальные проблемы математического моделирования». – Таганрог: Изд-во ТТИ ЮФУ, 2010, №6(107). С. 66-77.
5.Сухинов А.И., Чистяков А.Е. Адаптивный модифицированный попеременно-треугольный итерационный метод для решения сеточных уравнений с несамосопряженным оператором. Математическое моделирование, 2012, том. 24, №1. С.3-20.
6.Сухинов А.И. Модифицированный попеременно – треугольный метод для задач тепловодности и фильтрации// Вычислительные системы и алгоритмы. – Ростов – на– Дону: Изд-во РГУ,1984, С. 52-59.
7.Чистяков А.Е. Теоретические оценки ускорения и эффективности параллельной реализации ПТМ скорейшего спуска. Известия ЮФУ. Технические науки. Тематический выпуск «Актуальные проблемы математического моделирования». – Таганрог: Изд-во ТТИ ЮФУ, 2010, №6(107). С. 237-249.