Слабосвязанный алгоритм интегрированной инерциально-спутниковой навигационной системы транспортного средства
Аннотация
Дата поступления статьи: 12.08.2013Существующие подходы к тесной интеграции относительно дешевых бесплатформенных инерциальных навигационных систем (БИНС), построенных на основе MEMS-технологий, и спутниковых систем навигации (СНС) неэффективны применительно к автотранспортной технике. Рассмотрен итерационный алгоритм для слабосвязанного режима интеграции разнородных навигационных систем, не предполагающий использования методов оптимального оценивания. Решение получено на основе полной нелинейной модели навигационной системы наземного транспортного средства и, поэтому, справедливо для произвольного и неизвестного заранее характера его движения, причем, при самых общих предположениях об уровне действующих на него возмущений.
Ключевые слова: наземное транспортное средство, интегрированная инерциально-спутниковая навигационная система, итерационный слабосвязанный алгоритм
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
Известно, что относительно дешевые современные инерциальные навигационные системы (ИНС) не позволяют с достаточной точностью определять навигационные параметры движущихся объектов и, поэтому, для автотранспортных средств (ТС) требуемая точность чаще всего обеспечивается посредством комплексирования разнородных навигационных систем (НС) – недорогих бесплатформенных ИНС (БИНС) на основе MEMS-датчиков и спутниковых навигационных систем ГЛОНАСС/GPS [1,2]. Так как процессы оценивания навигационных параметров ТС осуществляются в реальном времени и должны учитывать динамику управляемых процессов, то существуют попытки построения алгоритмов интегрированных навигационных систем ТС из предположения о статистическом характере помех измерения, и, как следствие, основанных на различных методах оптимальной стохастической фильтрации [3-5]. Однако до настоящего момента существуют нерешенные проблемы практического использования подобных подходов именно применительно к автомобильной технике, так как траектории движения наземных транспортных средств заранее неизвестны, а о возможных возмущениях известны только самые общие предположения.
Во-первых, для построения универсальных математических моделей автотранспортных средств неприменим формализм Ньютона, на котором основаны процессы синтеза моделей оцениваемых объектов в классических задачах фильтрации, используемых для навигации других типов подвижных объектов, например, летательных аппаратов или морских судов [3,5-7].
Во-вторых, в подобных задачах также неэффективны и так называемые методы тесной интеграции, базирующиеся на выводе уравнений ошибок НС [3-5]. При допущении о малости погрешностей измерителей решение подобных уравнений, являющихся, по существу, уравнениями в вариациях и получаемых из уравнений основной задачи навигации, позволяет синтезировать асимптотическую оценку ошибок навигационной системы. Следовательно, неизбежные погрешности, обусловленные утратой нелинейных взаимосвязей при линеаризации уравнений и допущениями о малости как ошибок измерений, так и погрешностей линеаризации при использовании довольно грубых измерительных MEMS-датчиков БИНС автомобиля, будут обуславливать непреодолимые проблемы устойчивости синтезируемых фильтров. Кроме того, на сегодняшний день практически отсутствуют адекватные математические модели погрешностей MEMS-датчиков, возможные для использования в течение длительных временных интервалов эксплуатации транспортных средств без периодических калибровок. Поэтому известные многочисленные методы оценивания, общим необходимым условием применения которых является наличие априорной информации о моделях ошибок измерителей [4,5,8], здесь также не могут использоваться.
И, наконец, в-третьих, важнейшей особенностью спутниковых наблюдений является их дискретный характер. Соответственно, здесь решается уже задача непрерывно-дискретной фильтрации на основе совместного использования двух видов оценок: непрерывной – на интервале между спутниковыми наблюдениями, и дискретной – в момент приема навигационного сообщения. При этом также известно, что подобные комбинации непрерывных и дискретных фильтров имеют малые запасы устойчивости. Проблемным в этом случае является также и тот факт, что показания СНС могут иметь непредсказуемые "выбросы" – случайным неконтролируемым образом выдают неопознанную недостоверную информацию о местоположении ТС (например, при малом числе видимых навигационных спутников, когда автономные позиционные и скоростные спутниковые навигационные решения невозможны) [1,2,5].
По всей видимости, именно в связи с вышеперечисленным, методов эффективной, основанной на оптимальном оценивании, тесной интеграции грубых БИНС и СНС, применительно к автотранспортным средствам в настоящее время нет. В свою очередь, трудности алгоритмического обеспечения предопределяют неэффективность в целом использования бортовой интегрированной НС автотранспортного средства.
Поэтому представляет практический интерес рассмотренный ниже алгоритм слабой интеграции БИНС на основе MEMS-технологии и СНС, не предполагающий использования методов оптимального оценивания. Эффективность разработанного алгоритма объясняется использованием полной нелинейной модели объекта и, поэтому, решение справедливо для произвольного и неизвестного заранее характера движения ТС, причем, при самых общих предположениях об уровне действующих на него возмущений. Кроме того, рассмотренный алгоритм является универсальным для любого состава датчиков БИНС, включающего в общем случае как инерциальные, так и неинерциальные измерители (магнитометры, доплеровские датчики, и т.п.) любого класса точности и, соответственно, стоимости.
2 Исходные данные для решения
Предполагается, что на транспортном средстве (ТС) используется наиболее распространенная MEMS БИНС, построенная на трех акселерометрах, трех датчиках угловой скорости и трехосевом магнитном датчике. Для описания движения ТС используются следующие правые системы координат (СК) [9,10]:
- референцная СК, где за отсчетную поверхность принят эллипсоид Красовского (СК Пулково-42);
- геодезическая СК "Параметры Земли" (ПЗ-90), где за отсчетную поверхность принят общеземной эллипсоид;
- геодезическая СК "Мировая геодезическая система" (WGS-84);
- топоцентрическая СК ОENh, где положение центра масса (ц.м.) объекта задано геодезическими координатами – высотой места h, широтой j и долготой l, связанными с вектором ![]() нормальной силы тяжести [5];
нормальной силы тяжести [5];
- СК Cxyz, связанная с объектом (ССК), совершающая движение вместе с ним и ориентированная следующим образом: ось Cу направлена вдоль продольной оси автотранспортного средства, ось Сz лежит в плоскости (уz) симметрии объекта и перпендикулярна продольной оси, а ось Сх образует правый ортогональный трехгранник.
Также введены следующие ограничения и допущения. Во-первых предполагается, что автотранспортное средство движется только по автомобильным дорогам, отраженным в навигационных цифровых картах свободного доступа OpenStreetMap [2]. Во-вторых, пусть интегрированные ИНС и СНС работают в слабосвязанном режиме (Loosely Coupled Systems), когда решается задача коррекции БИНС при помощи позиционных автономных решений СНС [1,2]. При этом местоопределение центра масс движущегося объекта в СК ПЗ-90 СНС осуществляют с точностью, характеризуемой среднеквадратичным отклонением (СКО) 10 м. Также предполагается, что на временных интервалах до 5 мин могут иметь место вышеупомянутые случайные неконтролируемые и неопознанные "выбросы" СНС. В этих случаях точность определения координат ТС спутниковой системой характеризуется уже СКО, равным 200 м.
Исходной информацией навигационной системы являются, таким образом, измерения БИНС: составляющие ![]() вектора
вектора ![]() кажущегося ускорения автомобиля на оси ССК; составляющие
кажущегося ускорения автомобиля на оси ССК; составляющие ![]() вектора
вектора ![]() угловой скорости его вращения; угол курса Kи, рассчитываемый по измерениям магнитометра, а также координаты ТС в СК ПЗ-90 XСНС,YСНС и ZСНС, формируемые по измерениям СНС.
угловой скорости его вращения; угол курса Kи, рассчитываемый по измерениям магнитометра, а также координаты ТС в СК ПЗ-90 XСНС,YСНС и ZСНС, формируемые по измерениям СНС.
Выходной информацией навигационной системы являются широта φ и долгота λ положения автомобиля на поверхности Земли в СК Пулково-42.
3 Итерационный алгоритм решения навигационной задачи
Предлагаемый алгоритм интегрированной навигационной системы ТС представлен на рисунке. Алгоритм содержит два контура – быстрый, где автономно выполняется решение навигационной задачи БИНС, и медленный, где по показаниям СНС осуществляется коррекция решений БИНС и определяются начальные условия для первого такта последующего итерационного цикла быстрого контура.
Такт работы медленного контура
![]()
равен интервалу времени получения навигационных сообщений СНС. Здесь T0 – такт работы быстрого контура; kм>1 – коэффициент, определяемый из трудоемкости задач и производительности бортового вычислителя ТС.
В быстром контуре выполняется kм итерационных циклов решения навигационной задачи БИНС, где вычисляются текущие значения координат ТС φ, λ и h, восточная ![]() , северная
, северная![]() и вертикальная
и вертикальная ![]() составляющие линейной скорости ТС относительно Земли, а также углы пространственной ориентации ТС K, θ и ψ – курса, продольных и боковых наклонов соответственно. На схеме этой функциональной части решения задачи соответствует "Навигационный блок БИНС".
составляющие линейной скорости ТС относительно Земли, а также углы пространственной ориентации ТС K, θ и ψ – курса, продольных и боковых наклонов соответственно. На схеме этой функциональной части решения задачи соответствует "Навигационный блок БИНС".
Каждый цикл навигационного блока БИНС включает следующую последовательность действий. Для первого такта итерационного цикла T0 в качестве начальных данных используются выходные параметры медленного контура, остальные же исходные данные для (kм-1) последующих тактов формируются в ходе решения итерационных циклов классическим образом. Дискретность съема измерений датчиков БИНС равна при этом T0.
Вначале определяется матрица MC→E(0,i) (i= 1,2,…, kм) перехода из ССК в геодезическую СК ENh
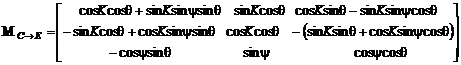 (1)
(1)
по начальным данным K, θ, ψ(θ,i), и элементы кососимметрической матрицы ![]()
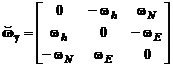 , (2)
, (2)
где ![]() ;
; ![]() ;
; ![]() ; Ω - угловая скорость суточного вращения Земли;
; Ω - угловая скорость суточного вращения Земли; 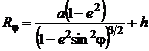 ;
; ![]() ; a, е – параметры эллипсоида Красовского; VE,VN,Vh, θ,h, λ(0,i) – входные параметры.
; a, е – параметры эллипсоида Красовского; VE,VN,Vh, θ,h, λ(0,i) – входные параметры.
Далее выполняется интегрирование матричного дифференциального уравнения Пуассона [5,8] для определения компонентов матрицы ![]() :
:
![]() , (3)
, (3)
где 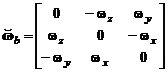 - кососимметрическая матрица, формируемая по текущим измерениям ДУСов.
- кососимметрическая матрица, формируемая по текущим измерениям ДУСов.
При вычислении текущих значений компенсационных ускорений ![]() пренебрегаем изменением вектора гравитационного ускорения на такте интегрирования и в расчетах используются значения φ, λ, VN, VE, Rφ, Rλ(t0,i-1), полученные на предыдущем шаге. Для этого вначале вычисляется величина нормальной силы тяжести на поверхности эллипсоида γ:
пренебрегаем изменением вектора гравитационного ускорения на такте интегрирования и в расчетах используются значения φ, λ, VN, VE, Rφ, Rλ(t0,i-1), полученные на предыдущем шаге. Для этого вначале вычисляется величина нормальной силы тяжести на поверхности эллипсоида γ:
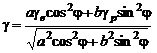 , (4)
, (4)
где ![]() - величины нормальной силы тяжести на земном экваторе и полюсе, равные
- величины нормальной силы тяжести на земном экваторе и полюсе, равные ![]() ,
, ![]() (м/с2).
(м/с2).
По величине g рассчитываются составляющие вектора ![]() действительной силы тяжести, представляющего собой сумму вектора
действительной силы тяжести, представляющего собой сумму вектора ![]() нормальной силы тяжести и вектора
нормальной силы тяжести и вектора ![]() аномалии силы тяжести:
аномалии силы тяжести:
![]() ;
; ![]() ;
; ![]() , (5)
, (5)
где ![]() - восточная и северная составляющие уклонения отвесной линии;
- восточная и северная составляющие уклонения отвесной линии; ![]() - аномалия силы тяжести.
- аномалия силы тяжести.
Тогда окончательно получаем:
![]() ;
;
![]() ; (6)
; (6)
![]() ,
,
где ![]() ;
; ![]() .
.
По измеряемым текущим значениям акселерометров nx,ny,nz вычисляются составляющие
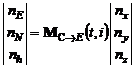 , (7)
, (7)
и, окончательно, находятся ускорения ТС в геодезической СК на i-м шаге итерационного цикла:
![]() ;
; ![]() ;
; ![]() . (8)
. (8)
Выходные параметры навигационного блока БИНС – текущие скорости и координаты ТС, определяются из уравнений:
![]() ;
; ![]() ;
;
![]() ; (9)
; (9)
![]() ;
; ![]() ;
;
![]() . (10)
. (10)
Также в быстром контуре рассчитывается среднее значение приращения модуля скорости на интервале kмT0 по измеренным акселерометрами ускорениям во всех kм тактах итерационного цикла:
![]() ; (11)
; (11)
где ![]() ; j – номер такта медленного контура.
; j – номер такта медленного контура.
Формируемое таким образом значение приращения модуля скорости характеризуется только погрешностями акселерометров и не содержит погрешности, обусловленной ошибками ДУСов.
Рассчитанные в kм-м цикле по уравнениям (9-11) текущие переменные вектора состояния ТС являются исходными данными для j-го такта медленного контура:
![]() ,
,
где также используются усредненные результаты измеренного магнитометром БИНС угла курса Kи на интервале kмTsub:
![]() . (12)
. (12)
В медленном контуре в первую очередь выполняются преобразования систем координат. Преобразование выходных значений быстрого контура – фазовых переменных ТС, из СК Пулково-42 в СК WGS-84 выполняется в три этапа. Вначале выполняется переход из геодезических координат в декартовые координаты СК Пулково-42 в соответствии с уравнениями
![]() ;
; ![]() ;
;
![]() ,
,
где ![]() – радиус кривизны первого вертикала,
– радиус кривизны первого вертикала,
а затем выполняется переход из декартовых координат Пулково-42 в декартовы координаты ПЗ-90 и, далее, в СК WGS-84 по известным уравнениям [10].
Одновременно выполняется преобразование из СК ПЗ-90 также в СК WGS-84 декартовых координат ТС, восстанавливаемых по измерениям СНС. В результате получаем две группы координат ТС в СК WGS-84 в одноименные моменты времени, но формируемые по результатам работы разнородных навигационных систем – БИНС ![]() ,
,![]() ,
,![]() и СНС
и СНС ![]() ,
,![]() ,
,![]() .
.
В медленном контуре учтено допущение, что ТС может совершать движение только по дорогам, координаты которых отражены в навигационных цифровых картах. Также, учтен тот факт, что может иметь неконтролируемое и никак не опознаваемое существенное ухудшение точности работы СНС, что и исключает возможность использования простейшей схемы раздельной интеграции (Separate Systems) грубой БИНС и СНС, когда автономные спутниковые навигационные решения просто заменяют соответствующую информацию инерциальной системы [1,2]. Поэтому далее выполняется прогноз местоположения ТС на автомобильной дороге.
Для этого вначале уточняется направление движения ТС по значению ![]() из уравнения (12). Затем угол курса корректируется по цифровой карте – по координатам дороги, что позволяет получить его точное текущее значение
из уравнения (12). Затем угол курса корректируется по цифровой карте – по координатам дороги, что позволяет получить его точное текущее значение![]() . За счет последнего появляется возможность расчета прогнозируемого перемещения ТС за прошедший интервал времени Tм:
. За счет последнего появляется возможность расчета прогнозируемого перемещения ТС за прошедший интервал времени Tм:
![]() . (13)
. (13)
Исходя из значений модуля скорости ![]() (11),
(11), ![]() (13) и скорректированного угла курса определяется окрестность возможного положения ТС на карте и выполняется выборка группы из m пар координат
(13) и скорректированного угла курса определяется окрестность возможного положения ТС на карте и выполняется выборка группы из m пар координат ![]() , описывающих траекторию дороги в окрестности данной точки.
, описывающих траекторию дороги в окрестности данной точки.
Решение задачи идентификации на основе минимизации невязок осуществляется в статистической (апостериорной) постановке – по результатам полученных наборов измерений относительно базового решения. В результате находятся координаты местоположения ТС ![]() . При выборе конкретного алгоритма идентификации основным является требование к его вычислительной эффективности [11].
. При выборе конкретного алгоритма идентификации основным является требование к его вычислительной эффективности [11].
С целью обеспечения возможности последующей работы итерационной схемы выполняется расчет начальных условий для следующего, j+1-го такта. Для этого осуществляется обратный перевод полученных координат ТС из СК WGS-84 в декартовые координаты Пулково-42, а затем и в геодезические координаты, для чего необходимо проведение итераций при вычислении геодезической широты и геодезической высоты [10].
По формируемым таким образом значениям φ,h, λ(0, j+1) находятся и остальные фазовые переменные из уравнений:
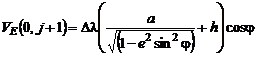 ;
;
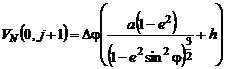 ; (14)
; (14)
![]() ,
,
где ![]() ;
; ![]() .
.
Для окончательного формирования начальных данных для быстрого контура следующего j+1-го такта итерационной схемы необходимо найти оставшиеся углы, используемые для расчета начальной матрицы MC→E(0,i):
![]() ;
; 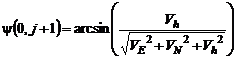 . (15)
. (15)
Заключение
Рассмотренный алгоритм решения навигационной задачи автомобиля обеспечивает возможность эффективной интеграции БИНС на основе MEMS-технологии и СНС. Такое построение вычислений позволяет избежать накопления ошибок интегрирования и увеличения погрешностей местоположения ТС со временем. Как показало моделирование, этот факт обеспечивает достаточную – субметровую, точность работы схемы, причем, без привлечения аппарата оптимальной фильтрации.
Необходимо еще раз отметить то, что предложенный слабосвязанный алгоритм интегрированной навигационной системы базируется на использовании полной нелинейной модели объекта и, поэтому, справедлив для произвольного и неизвестного заранее характера его движения.
Результаты исследований, изложенные в данной статье, получены при финансовой поддержке Минобрнауки РФ в рамках реализации проекта «Создание высокотехнологичного производства для изготовления комплексных реконфигурируемых систем высокоточного позиционирования объектов на основе спутниковых систем навигации, локальных сетей лазерных и СВЧ маяков и МЭМС технологии» по постановлению правительства №218 от 09.04.2010 г. Исследования проводились в ФГАОУ ВПО ЮФУ.
Список литературы:
- Пешехонов, В.Г. Интегрированные инерциально-спутниковые системы навигации: сб. ст. и докл. [Текст] – СПб.: Электроприбор, 2001. – 235 с.
- Sukkarieh, S. Low Cost, High Integrity Aided Inertial Navigation Systems For Autonomous Land Vehicles [текст]: Ph.D. Thesis, Univ. of Sydney, 2000. – 136 p.
- Голован А.А., Парусников Н.А. Математические основы навигационных систем. Ч. I. Математические модели инерциальной навигации [Текст] – М.: МГУ, 2010. – 126 с.
- Демидов, О.В. Задача тесной интеграции систем ГЛОНАСС и GPS с ИНС разных классов точности [Текст]: Дисс. на соиск. степ. к.ф.-м.н.: 01.02.01 : защищена 11.12.2009 / Голован Андрей Андреевич. – М.: МГУ, 2009. – 139 с.
- Анучин О.Н., Емельянцев Г.И. Интегрированные системы ориентации и навигации для морских подвижных объектов [Текст] – СПб.: Электроприбор, 2003. – 390 с.
- Weston, J. L. Basic Principles Of Strapdown Inertial Navigation Systems [Текст] // J. L. Weston // Strapdown Inertial Navigation Technology – 2nd Edition. – Radar, sonar, navigation and avionics, 2004. – Chapter 3. – P. 17-59.
- Середа А. Ю., Детюк К. В. Бортовой информационно-навигационный комплекс КА «ГЛОНАСС-К» [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/906 (доступ свободный)- Загл. с экрана. – Яз. рус.
- Красовский, А.А. Справочник по теории автоматического управления [Текст] – М.: Наука, 1987. – 712 с.
- Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных навигационных систем [Текст] – М.: Наука, 1979. – 320 с.
- ГОСТ Р 51794-2001. Аппаратура радионавигационная глобальной навигационной спутниковой системы и глобальной системы позиционирования. Системы координат. Методы преобразования координат определяемых точек. – 12 с.
- Клевцов С.И. Моделирование алгоритма краткосрочного прогнозирования изменения быстроизменяющейся физической величины в реальном времени [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/920 (доступ свободный)- Загл. с экрана. – Яз. рус.