Распространение акустических волн в водопроводных сетях с изменяющимся диаметром труб
Аннотация
В работе рассмотрен случай, когда источник акустического сигнала находится внутри составной цилиндрической трубы. Показано, что при переходе трубы одного диаметра в трубу другого диаметра, целесообразно применить модальное представление акустической волны для каждого участка трубы.
Ключевые слова: акустика, контроль, диаметр, водопровод
Информация относительно текущего структурного состояния локальных магистральных водопроводных сетей, в совокупности с статистически выведенными эмпирическими моделями отказов, может увеличить долговечность эксплуатации водоводов и позволит управлять системами водоснабжения рентабельным способом.
Оценка состояния магистральных водопроводных сетей и соответственно принятия решения по восстановлению водопровода состоит из нескольких этапов: моделирование водопровода в наземном и подземном вариантах прокладки; оценка состояний водопровода при помощи средств измерительной техники, в том числе дефектоскопия труб; интерпретация измеренных показателей, определяющих текущее состояние водопровода; эмпирическое моделирование отказов в распределительных магистральных сетях малого диаметра; определение срока службы водопровода; оценка последствий аварийных отказов; планирование затрат для полного срока эксплуатации водопровода (количество, качество, надежность, и т.д.).
Определение условий эксплуатации водопровода не должно ориентироваться только на параметры, характеризующие аварийную ситуацию. Также важна информация о свойствах грунта; климате; грунтовых водах; покрывающих пластах; типе датчика, контролирующего данные о состоянии водопровода; конфигурации и геометрии трубы и т.п.
В работах [1,2] рассмотрено распространение акустической волны, распространяющейся внутри водопроводной трубы постоянного диаметра.
Рассмотрим целесообразность применения метода модального представления акустической волны [3], если осуществляется переход трубы одного диаметра в трубу другого диаметра рис. 1. Моды распространяющейся акустической волны различны, поэтому необходимо преобразовать акустическое давление в трубе одного диаметра в акустическое давление трубы другого диаметра, используя условия непрерывности акустического давления и скорости.
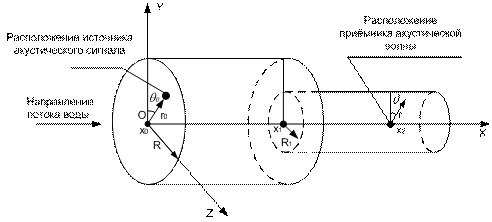
Рис. 1 – Вид составной трубы.
В работе учитываем, что условия непрерывности давления и скорости будут невыполнимы только для переданного поля акустического давления в трубу меньшего диаметра, так как часть поля будет отражена от краёв соединения двух труб.
Радиус рассматриваемой трубы ![]() на интервале
на интервале ![]() и
и ![]() на интервале
на интервале ![]() , причём
, причём ![]() >
>![]() . Предполагаем наличие круговой симметрии, поэтому исключаем появление мод вызванных неоднородностями трубы. Тогда на интервале
. Предполагаем наличие круговой симметрии, поэтому исключаем появление мод вызванных неоднородностями трубы. Тогда на интервале ![]() с учетом выражения приведенного в [2] акустическое давление имеет вид:
с учетом выражения приведенного в [2] акустическое давление имеет вид: ![]() .
.
В точке ![]() происходит рассеяние акустической волны, на отраженную волну
происходит рассеяние акустической волны, на отраженную волну ![]() , и на переданную волну
, и на переданную волну ![]() , где
, где ![]() ;
; ![]() ;
; ![]() ;
; ![]() и
и ![]() являются обобщениями
являются обобщениями ![]() и
и ![]() на интервале
на интервале ![]() .
.
Принимаем условия сходимости бесконечного ряда для радиального и аксиального волнового числа отраженной волны ![]() ; и радиального и аксиального волнового числа прошедшей волны
; и радиального и аксиального волнового числа прошедшей волны ![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Матрицы M и S показывают, что моды сформированной и распространяющейся акустической волны отражаются и передаются по трубе. Вектор A характеризует сформированную акустическую волну на начальном этапе, векторы D и C характеризуют области передачи и отражения.
Зададим граничные условия. В точке ![]() интервал
интервал ![]() действует условие непрерывности прижимной и осевой скоростей, а на краях отсутствует любой источник акустического сигнала. Тогда получаем уравнение непрерывности акустического давления
действует условие непрерывности прижимной и осевой скоростей, а на краях отсутствует любой источник акустического сигнала. Тогда получаем уравнение непрерывности акустического давления ![]() и уравнение непрерывности осевой скорости акустической волны
и уравнение непрерывности осевой скорости акустической волны ![]() (
(![]() если
если ![]() ,
, ![]() если
если ![]() ).
).
Проведем расчет акустического давления, распространяемого внутри трубы, с помощью интерактивной системы MatLab. Труба водопроводная напорная из полиэтилена диаметр 200мм и 100мм. Координаты источника акустического сигнала (![]() мм,
мм, ![]() ,
, ![]() м); координаты приёмника акустической волны (
м); координаты приёмника акустической волны (![]() мм,
мм, ![]() ,
, ![]() м); плотность воды 1000кг/м3; скорость звука в воде 1500м/с; расстояние до приёмника акустической волны х1=100м; расстояние до изменения диаметра трубы 50м.
м); плотность воды 1000кг/м3; скорость звука в воде 1500м/с; расстояние до приёмника акустической волны х1=100м; расстояние до изменения диаметра трубы 50м.
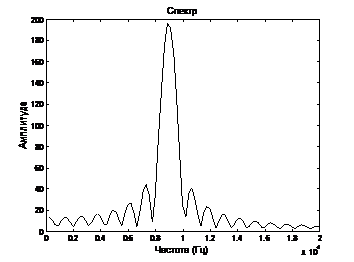
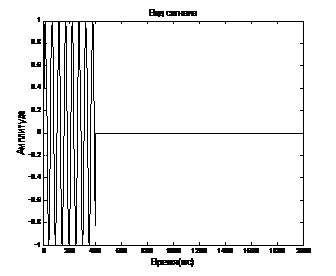
На рис. 2 приведен излучаемый ультразвуковой сигнал с частотой 55кГц и его спектр. Временные области распространения акустического давления для заданного сигнала, приведены на рис. (3-5).
 |
|
а) б)
Рис. 2 – Заданный сигнал (а) и его спектр (б)
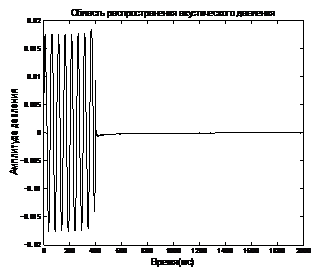
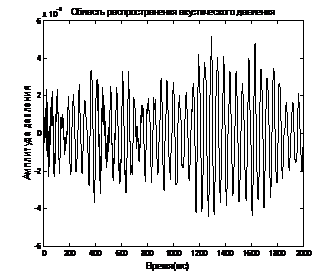
Рис. 3 –Область распространения акустического давления, х=100м, мода (0,0)
 |
|
а) б)
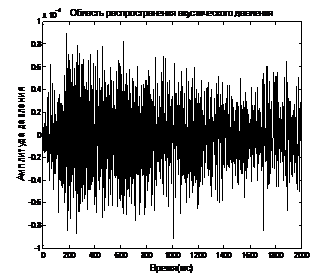
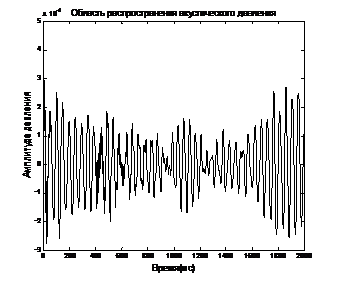
Рис. 4 – Временные области распространения акустического давления
мода (1,0) (а), мода (2,0) (б), х=100м
 |
|
а) б)
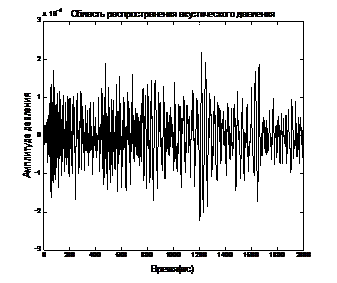
Рис. 5 – Временные области распространения акустического давления
мода (1,1) (а), мода (2,2) (б), х=100м
Прохождение акустической волны внутри трубы при изменении её диаметра к затуханию плоской волны мода (0,0) примерно в 100 раз (рис. 3). Таким же образом изменение диаметра трубы влияет и на более медленные моды (рис. 4-5), которые искажены из-за результата перекрытия волн, у которых есть более длинные пути распространения.
Таким образом, можно сделать вывод, что полученные уравнения непрерывности акустического давления и осевой скорости акустической волны позволяют определить величину акустического давления на границе перехода от трубы одного диаметра в трубу другого диаметра, что в свою очередь даст возможность обнаружить несанкционированные врезки в водопроводной сети; изменение геометрии трубы, вызванной осадочными налетами, коррозионными процессами и т.д.
Литература
1. Зибров, В.А., Сапронов, А.А. Использование пьезоэлектрических преобразователей для передачи информации о потребляемых водных ресурсах [Текст]// Энергосбережение и водоподготовка. Научно-технический журнал, 2009 - №3. - С. 78-81.
2 Сапронов, А.А., Зибров, В.А., Занина, И.А., Соколовская, О.В.. Исследование процесса передачи информации по акустическому каналу в водопроводе [Текст]// Энергосбережение и водоподготовка. Научно-технический журнал, 2012. – №4. – С.52-54.
3. Блохинцев, Д.И. Акустика неоднородной движущейся среды. – 2-е изд. – М.: Наука. Главная редакция физико-математической литературы, 1981. – 206 с.