Система мультидиагностики для больных с постуральным дефицитом и разработка алгоритма распознавания стабилографических сигналов
Аннотация
Работа связана с решением задачи синтеза информационных моделей поведения групп биомедицинских автономных интеллектуальных агентов и исследования методов машинного обучения обеспечивающих повышение достоверности прогноза их поведения с помощью многоагентных систем на основе применения бионических принципов, методов и моделей роевого интеллекта. Разработанная многоагентная система моделирует поведение групп автономных интеллектуальных агентов по разработанной методике, удовлетворяя предложенным критериям достоверности, отличаясь сформированной структурой системы и набором разработанных специализированных агентов, что обеспечивает возможности для моделирования системы биомедицинской групповой робототехники с помощью автономных интеллектуальных агентов. Разработан классификатор стабилографических сигналов по методу Парзена. Приведённые данные свидетельствуют о том, что вспомогательные признаки, полученные в результате многомерного шкалирования значительно информативнее исходных признаков.
Ключевые слова: Интеллектуальный агент, мультидиагностика, классификатор Парзена
05.11.17 - Приборы, системы и изделия медицинского назначения
Агентное моделирование может быть реализовано с помощью многоагентной системы [1]. Хотя традиционно в рамках таких систем исследуются интеллектуальные агенты, в роли их агентов также могут выступать и роботы. В условиях необходимости реализации агентного моделирования поведения групп биомедицинских роботов будет актуальна разработка многоагентной системы. Кроме того, в ходе агентного моделирования необходимо решение задачи по определению структуры и типов.Решение задачи качественной программной реализации многоагентных систем, состоящих из групп автономных интеллектуальных агентов на основе усовершенствованных методов моделирования поведения, является актуальным.
Имеет место противоречие между недостатками существующего аппарата моделирования многоагентных систем и требованиями в области достоверности прогнозирования поведения групп автономных интеллектуальных агентов. Так как классическое программирование применительно к группам роботов является сложной задачей, возникла необходимость в альтернативном подходе. Если исключить применение эволюционных или обучающих алгоритмов, единственно возможным является модельный подход. Основной его идеей является обеспечение поддержки разработчика алгоритма с помощью инструмента, который сможет прогнозировать поведение, заданное исполняемым алгоритмом, с наивысшей возможной точностью и в кратчайший период времени.
Базовая модель расположения роботов основана на принципе броуновского движения и составлена из пар соответствующих уравнений [2]. С одной стороны, используется уравнение Ланжевена, дифференциальное уравнение со стохастическими производными (1). С помощью него дается локальное, или микроскопическое описание конкретных траекторий.
![]() , (1)
, (1)
где ![]() - местоположение;
- местоположение;![]() - время;
- время;![]() – смещение;
– смещение;![]() – коэффициент диффузии;
– коэффициент диффузии;![]() – нормализованная шумовая составляющая.
– нормализованная шумовая составляющая.
На рисунке 1 представлена иллюстрация уравнения (1) с помощью четырех одномерных траекторий, начинающихся при r = 0, со смещением и без него.
С другой стороны, применяется уравнение Фоккера-Планка (прямое уравнение Колмогорова), дифференциальное уравнение с частными производными (2), которое может быть аналитически выведено из уравнения Ланжевена. Оно с помощью плотностей распределения вероятностей дает глобальное, или макроскопическое описание.
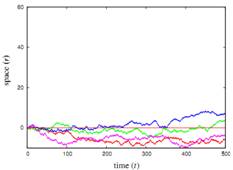
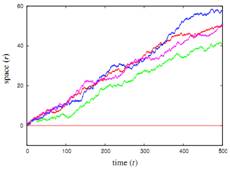
а) Четыре траектории при А = 0. б) Четыре траектории при A = 0.1.
Рисунок 1 –Траектории, построенные с помощью уравнения Ланжевена в одном измерении
![]() , (2)
, (2)
где ![]() – вероятность появления частицы в местоположении
– вероятность появления частицы в местоположении ![]() внутри прямоугольника, заданного
внутри прямоугольника, заданного ![]() в момент времени
в момент времени ![]() ;
;![]() - дифференциальный оператор.
- дифференциальный оператор.
Уравнение (2) проиллюстрировано на рисунке 2, изображающем плотность распределения вероятности ρ в одномерном пространстве при смещении A = 0.1, диффузии B = 0.6, и установке, близкой к δ-функции в r = 0. Линия r = At = 0.1t показывает траекторию наивысшей вероятности.

Рис. 2. Плотность распределения вероятности в одномерном пространстве, вычисленная с помощью уравнения Фоккера-Планка
На рисунке 3 изображена плотность распределения вероятности ρ, описывающая вероятность встречи частицы, начавшей движение в момент времени t=0 и r=0 в заданной точке в одномерном пространстве, рассчитанную с помощью уравнения Фоккера-Планка для смещения A = 0,1 и диффузии B=0,3. На плоскость rt нанесены четыре траектории, рассчитанные с помощью соответствующего уравнения Ланжевена.
В рамках данной работы физическая модель расширяется до обобщенной модели сообщающихся групп роботов, основанной на эвристических рассуждениях. Такой модельный подход имеет большое количество применений, однако адаптация к специальному алгоритму управления требует отдельного этапа моделирования.
Проблема выделения информативных признаков сигнала сама по себе является далеко не тривиальной. Эффективное решение этой проблемы может быть достигнуто только путём разработки адекватной математической модели, устанавливающей формальные взаимосвязи параметров анализируемого сигнала с параметрами порождающей его системы. В настоящей работе приводятся результаты исследований, связанных с разработкой алгоритмов распознавания стабилографических сигналов в рамках концепции перевёрнутого маятника, подробно описанной в [3].
В условиях поставленной задачи наиболее высокое качество классификации могут обеспечить метрические классификаторы [4], использующие минимум априорной информации о структуре обучающей выборки и рассматривающие каждый её элемент, как прецедент с особой диагностической ценностью. Прецедентная логика работы метрических алгоритмов хорошо понятна экспертам в различных предметных областях, что без сомнения является их важным преимуществом перед другими методами классификации. Наиболее общей формой метрического классификатора является парзеновский классификатор, основанный на получении локальных оценок плотности вероятностей. Его можно рассматривать так же как непараметрический вероятностный классификатор. Согласно методу Парзена [5] локальная оценка плотности распределения вероятности для каждого из классов Сj в точке, соответствующей классифицируемому наблюдению Х находится как
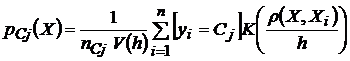 , (1)
, (1)
где K–функция ядра, h–ширина окна, nCj–число элементов класса Сj, ρ – мера сходства (метрика), V(h) – нормирующий множитель, определяемый как
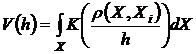 . (2)
. (2)
В действительности при классификации методом парзеновского окна в вычислении V(h) нет никакой необходимости, так как при оценке апостериорной вероятности принадлежности наблюдения к классу Сj по формуле
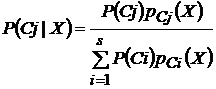 , (3)
, (3)
где s – число классов, этот сомножитель сокращается.
Таким образом, для построения парзеновского классификатора требуется определить оптимальную функцию ядра, а также задать оптимальную метрику на рассматриваемом признаковом пространстве
Для предварительного анализа признакового пространства использовались глобальные оценки АR- параметров стабилографических сигналов, средней длительностью 1500 отсчётов, записанные для здоровых пациентов, при поддержании ими равновесия с открытыми и закрытыми глазами. Всего было обследовано 20 пациента, в результате чего сформирована матрица данных размерами 8х40.
На рисунке 1 приведены распределения анализируемых наблюдений в координатах наиболее информативных признаков, полученных для разных признаковых пространств. Данный рисунок подтверждает адекватность манхэттенской метрики реальным данным, так как при её использовании возможно наиболее эффективное разделение классов. На рисунке видно, что оптимальная разделяющая линия в случае манхэттенской метрики наклонена по отношению к оси а8 почти на 450, в то время как в случае евклидовой метрики эти линии почти перпендикулярны. Этим объясняется более высокое значение R2 для евклидовой метрики.
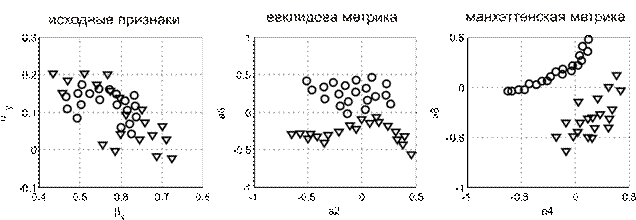
Рисунок 1 – Распределение стабилографических сигналов в координатах наиболее информативных признаков для различных признаковых пространств(о – глаза открыты, ∇- глаза закрыты)
Для снижения влияния неоднородности выборки на результаты классификации в классификаторе используются парзеновские окна переменной ширины, ограничивающее фиксированное количество наблюдений. Оптимальное количество ближайших соседей, используемых для классификации, определялось по методу скользящего контроля. На рисунке 2 представлены результаты скользящего контроля в группе измерений с открытыми глазами.
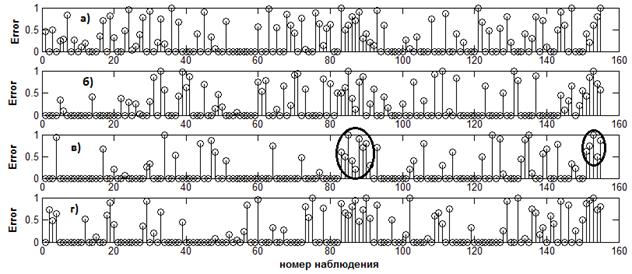
Рисунок 2 – Результаты скользящего контроля в группе измерений с открытыми глазами для различного числа наблюдений, ограниченных парзеновским окном
а) k=1, Error ср.=0,28; б) k=3, Error ср.=0,23; в) k=5, Error ср.=0,17; г) k=7, Error ср.=0,24
Как следует из рисунка, наилучшая классификация достигается при использовании парзеновского окна, ограничивающего 5 ближайших соседей.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 гг., мероприятие 1.4, соглашение от 14.11.2012 г. № 14.A18.21.2081.
Литература
- Michael Wooldridge, An Introduction to MultiAgent Systems, John Wiley & Sons Ltd, 2002. – 366 p.
- Hamann H. Space-Time Continuous Models of Swarm Robotic Systems, Cognitive Systems Monographs, volume 9, Springer-Verlag Berlin Heidelberg, 2010.
- Киреев А.В., Акжигитов Р.Ф. Моделирование основных закономерностей формирования стабилографических сигналов в рамках концепции перевёрнутого маятника / Известия ЮФУ. Технические науки. Тематический выпуск. «Медицинские информационные системы» №9(134). – Таганрог, 2012. –С. 114-119.
- Журавлев Ю. И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. – 159 c.
- Parzen E. On the estimation of a probability density function and mode // Annals of Mathematical Statistics. - 1962. - Vol. 33. - Pp. 1065–1076.