Определение скоростей движения охлажденного воздуха при открывании дверей шкафа бытового холодильного прибора
Аннотация
Рассматривается вопрос истечения охлажденного воздуха при открытии дверей шкафа бытового холодильника, с целью определения величины энергетических потерь, связанных с замещением охлажденного воздуха теплым. Сделана попытка математически описать законы движения потока охлажденного воздуха для различных условий эксплуатации холодильника, включая форму и скоростные характеристики потока.
Выполнен поиск решений уравнений математической физики, описывающих свободное истечение холодного потока воздуха с учетом его геометрии и временных изменений.
Сделав ряд допущений, разработана модель движения охлажденного воздуха, обеспечивающая возможность решать инженерные задачи по оценке характеристик потока для конкретных физических условий.
Ключевые слова: бытовой холодильник, движение холодного воздуха, энергосбережение, параметры потока.
На рынке бытовой техники наибольший объем продаж составляют бытовые холодильники и морозильники. Общая численность холодильников и морозильников в домохозяйствах России в 2005-2009 годы колебалась от 63,68 до 67,69 млн. штук. Около 90% рынка бытового холодильного оборудования занимают холодильники.
Доля пользователей холодильников и морозильников стабильно составляет 99,7-99,8% от всех домохозяйств [1].
Исходя из вышесказанного, вопросы энергосбережения при эксплуатации бытовых холодильников являются актуальными, при этом важным является решение задачи снижения эксплуатационных потерь, обусловленных открыванием дверей холодильных и морозильных камер.
Задача свободного истечения холодного воздуха из шкафа бытового холодильного прибора без учета влияния на поток внешних сил необходима для решения задач снижения энергопотребления. Истекающий из камеры холодный воздух, имея большую плотность, чем воздух в помещении, свободно перемещается вниз.
Задача свободного истечения воздуха описывается следующей системой уравнений [2]:
1). Уравнение Менделеева – Клапейрона:![]() (1)
(1)
где: ![]() универсальная газовая постоянная;
универсальная газовая постоянная;![]() удельный объем газа;
удельный объем газа;![]() давление и температура газа в каждой точке потока.
давление и температура газа в каждой точке потока.
2). Коэффициент теплопроводности газа «![]() » пропорционален коэффициенту динамической вязкости «
» пропорционален коэффициенту динамической вязкости «![]() » и выполняется критерий Прандтля:
» и выполняется критерий Прандтля: ![]() (2)
(2)
3). Уравнение неразрывности движения: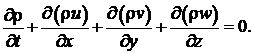 (3)
(3)
4). Основные уравнения Навье — Стокса динамики вязкого газа, отнесенные к единице массы: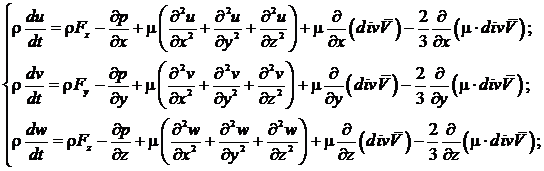 (4)
(4)
здесь: ![]() проекции вектора скорости
проекции вектора скорости ![]() на оси ОХ, ОУ, ОZ;
на оси ОХ, ОУ, ОZ;![]() вектор внешних объемных сил, действующих на газ в каждой точке пространства;
вектор внешних объемных сил, действующих на газ в каждой точке пространства;![]() коэффициент динамической вязкости;
коэффициент динамической вязкости;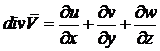 . (5)
. (5)
Основные допущения задачи истечения потока воздуха из холодильной камеры:
1). Внешние силы на воздушный поток внутри холодильника не влияют. Для данной модели можно рассмотреть допущение:![]() (6)
(6)
где ![]() ускорение силы тяжести.
ускорение силы тяжести.
2). Коэффициент удельной теплоемкости «![]() » не зависит от абсолютной температуры газа и является физической константой газа.
» не зависит от абсолютной температуры газа и является физической константой газа.
3). При истечении газа учитывается только динамическая вязкость первого рода (сопротивление окружающего теплого воздуха потоку холодного воздуха).
4). Газ представляет собой «ньютоновскую» среду, подчиненную
известному обобщенному закону Ньютона о линейной связи между тензором напряжений и тензором скоростей деформаций.
Граничные условия задачи:
1). Скорости потока на неподвижной твердой границе внутри холодильного шкафа равны нулю.
2). Начальные скорости истечения холодного воздуха из шкафа направлены вдоль продольной оси и по величине равны ![]() в каждой точке нижней трети высоты прямоугольного сечения на выходе из шкафа.
в каждой точке нижней трети высоты прямоугольного сечения на выходе из шкафа.
3). Задана температура воздуха внутри шкафа в начальный момент времени истечения холодного воздуха из шкафа и равна ![]() .
.
4). В начальный момент времени температура снаружи холодильного шкафа постоянна и равна ![]() .
.
5). Скорости воздушных масс снаружи холодильного агрегата в начальный момент открывания двери в каждой точке пространства равны нулю.
Для упрощения задачи истечения холодного воздуха из холодильного шкафа принимаем, что процесс истечения воздуха является изотермическим и стационарным по времени. Это условие означает, что исключается диффузионный процесс перемешивания холодного (свободно истекающего) воздуха и теплого (комнатного). Также полагаем, что вытекающий холодный воздух есть несжимаемая среда, а также то, что изменения параметров потока в направлении поперечной горизонтальной оси не происходит (рис.1.а) и тогда реальный трехмерный поток заменяется двумерным (рис. 1.б). Дополнительно полагаем, что силы вязкости пропорциональны квадрату модуля скорости.
При сделанных допущениях уравнение неразрывности выполняется и основная система уравнений движения потока примет следующий вид: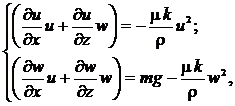 (7)
(7)
здесь ![]() коэффициент пропорциональности, зависящий от формы потока, определяется экспериментально.
коэффициент пропорциональности, зависящий от формы потока, определяется экспериментально.
Система (7) является базовой для нахождения скоростей потока при его свободном истечении из холодильной камеры в стационарном режиме.
В стационарном режиме на выходе из шкафа вектор скорости потока обладает некоторой продольной (горизонтальной) составляющей «![]() », при этом вертикальная составляющая «
», при этом вертикальная составляющая «![]() » равна нулю. Начальная составляющая вектора скорости может определяться экспериментально и, таким образом, ее значение на выходе будет являться заданным. Не учитывая сопротивление дна холодильной камеры воздушному потоку, можно полагать, что на выходе из шкафа поток движется равномерно:
» равна нулю. Начальная составляющая вектора скорости может определяться экспериментально и, таким образом, ее значение на выходе будет являться заданным. Не учитывая сопротивление дна холодильной камеры воздушному потоку, можно полагать, что на выходе из шкафа поток движется равномерно: ![]() (8)
(8)
Значение вертикальной проекции вектора скорости на выходе из холодильной камеры будем полагать равным нулю:![]() , (9)
, (9)
а ускорение потока на выходе из холодильной камеры будет равно:![]() . (10)
. (10)
Вытекая, из шкафа, поток начинает тормозиться в направлении оси ОХ в силу вязкости среды, то есть продольная составляющая вектора скорости обладает свойствами: ![]()
![]() (11)
(11)
При этом функция ![]() должна быть монотонно убывающей как по переменной «
должна быть монотонно убывающей как по переменной «![]() », так и по переменной «
», так и по переменной «![]() ».
».
Вертикальная проекция вектора скорости потока на выходе из шкафа будет вначале возрастать из-за силы тяжести, действующей на поток, которая возникает в силу его более высокой плотности чем окружающего воздуха.
Однако, по мере возрастания вертикальной составляющей «![]() » возрастает и сила сопротивления вязкой среды, соответственно через некоторое время сила тяжести воздушного потока, направленная вертикально вниз, будет уравновешена силой сопротивления среды, соответственно вертикальная составляющая потока «
» возрастает и сила сопротивления вязкой среды, соответственно через некоторое время сила тяжести воздушного потока, направленная вертикально вниз, будет уравновешена силой сопротивления среды, соответственно вертикальная составляющая потока «![]() » будет стремиться к некоторому постоянному значению, которое может быть определено экспериментально:
» будет стремиться к некоторому постоянному значению, которое может быть определено экспериментально:![]() . (12)
. (12)
При этом функция ![]() должна быть монотонно возрастающей по переменной «
должна быть монотонно возрастающей по переменной «![]() » и монотонно убывающей по переменной «
» и монотонно убывающей по переменной «![]() ».
».
Будем теперь находить приближенные решения системы (7), удовлетворяющие условиям (8) – (12). Соответствующая этим условиям структура решения системы (7) имеет вид: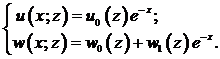 (13)
(13)
Для последующего нахождения решений систему (7) удобно преобразовать к виду: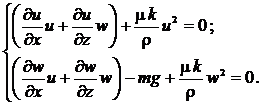 (14)
(14)
Подставим выражения (13) в систему (14), найдем необходимые производные и сгруппируем слагаемые в левой части каждого из уравнений по степеням ![]() . После упрощений получим:
. После упрощений получим: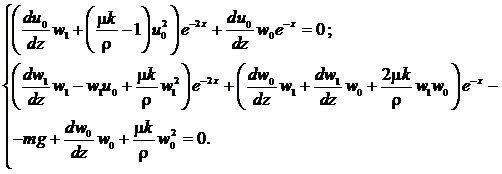 (15)
(15)
Функции ![]() будем определять из тех условий, чтобы каждый множитель при
будем определять из тех условий, чтобы каждый множитель при ![]() в уравнениях системы (15) был или равен нулю, или принимал значения, близкие к нулю, соответственно оба уравнения системы (15) будут приближенно выполнены.
в уравнениях системы (15) был или равен нулю, или принимал значения, близкие к нулю, соответственно оба уравнения системы (15) будут приближенно выполнены.
Приравняем сначала к нулю выражение: 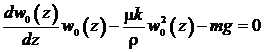 . (16)
. (16)
Общее решение уравнения (16) находится с помощью [3] и имеет вид: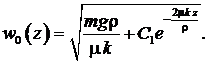 (17)
(17)
Приравнивая к нулю коэффициент при ![]() во втором уравнении системы (16), получим:
во втором уравнении системы (16), получим: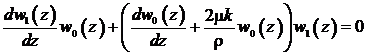 . (18)
. (18)
Находим общее решение уравнения (18):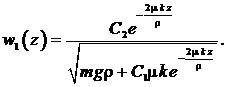 (19)
(19)
Функцию ![]() будем определять из условия равенства нулю коэффициента при
будем определять из условия равенства нулю коэффициента при ![]() в первом уравнении системы (16):
в первом уравнении системы (16):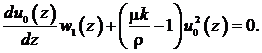 (20)
(20)
Уравнение (20) является уравнением с разделяющимися переменными относительно неизвестной функции ![]() , его общее решение имеет вид:
, его общее решение имеет вид: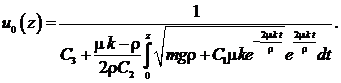 (21)
(21)
Учитывая (13), (21), получим выражение модельной функции ![]() :
: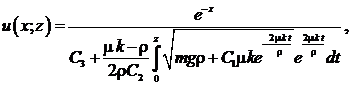 (22)
(22)
Выражение для модельной функции ![]() следует из (13), (17), (19):
следует из (13), (17), (19):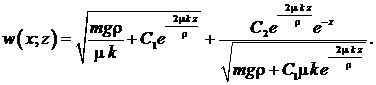 (23)
(23)
Найдем значения произвольных постоянных ![]() решая задачу Коши.
решая задачу Коши.
Для определения постоянной ![]() воспользуемся уравнением (22), в котором подставим в обеих частях равенства
воспользуемся уравнением (22), в котором подставим в обеих частях равенства ![]() и
и ![]() . Получим:
. Получим: 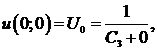 отсюда
отсюда 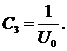 (24)
(24)
Полагая в (23) также значения переменных ![]() и
и ![]() , имеем:
, имеем: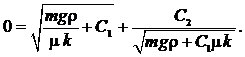 (25)
(25)
Из уравнения (25) выразим постоянную ![]() через
через ![]() :
: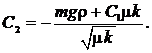 (26)
(26)
Для нахождения константы ![]() дифференцируем функцию (23) по переменной «
дифференцируем функцию (23) по переменной «![]() » и подставляя значения
» и подставляя значения ![]() и
и ![]() , находим:
, находим: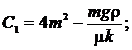
![]() . (27)
. (27)
Таким образом, проекции вектора скорости определяются по формулам (22), (23), где постоянные ![]() определяются по формулам (24), (27).
определяются по формулам (24), (27).
Масса вытекающего воздуха пропорциональна плотности «![]() ». Плотность воздуха при
». Плотность воздуха при ![]() при
при ![]() следовательно масса
следовательно масса ![]() пропорциональна
пропорциональна ![]()
Из эксперимента было получено, что значения ![]() и
и ![]() равны:
равны:![]() и
и ![]() .
.
Рассогласование значений скоростей потока в эксперименте и полученных по формулам (22), (23) не превышает 15 %.
Литература.
- 1. Анализ рынка холодильников и морозильников в России в 2006-2010 гг, прогноз на 2011-2015 гг. ООО «Бизнес Статистика» http://businesstat.ru,
2. Лойцянский, Л.Г. Механика жидкости и газа [Текст] / Л.Г. Лойцянский. – 5-е изд. – М.: Наука, 1978. – 736 с.
3. Корн, Г. Справочник по математике для научных работников и инженеров [Текст] / Г. Корн, Т. Корн. – М.: Наука, 1970. – 720 с.