Двумерная математическая модель жидкости водоема с учетом наличии на поверхности ледяной пластины
Аннотация
Данная статья рассматривает задачу построения двумерной гидродинамической модели области водоема с учетом наличия ледового покрытия, плавающего на поверхности. Численная модель является двумерной (в вертикальной плоскости), решение основывается на уравнениях Навье-Стокса в приближениях. Для построения численного алгоритма применяется метод расщепления по физическим процессам.
Ключевые слова: Ледяная пластина, ячейка, волновая гидродинамика, уравнений движения жидкости, уравнений неразрывности, заполненность.05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение. В данной работе рассматривается численная модель движения в двумерных (в вертикальной плоскости) водоемах. Математическая модель основана на уравнениях Навье-Стоксавприближениях. Для построения численного алгоритма применяются метод расщепления по физическим процессам.
1. Постановка задачи. Рассматривается задача волновой динамики жидкости. Исходными уравнениями являются:
– уравнение Навье-Стокса:![]() ; (1)
; (1)
. ![]() (2)
(2)
– уравнение неразрывности:![]() (3)
(3)
Уравнения (1) – (3) рассматриваются при следующих граничных условиях, где для разных границ данной области жидкости отдельные условия
– на дне водоема:![]() (4)
(4)
– на свободной поверхности жидкости:![]() ,
,![]() ; (5)
; (5)
– на поверхности жидкости, покрытой ледяной пластиной: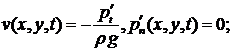
![]() ,
,![]() ,
,
– на входе задается поток от источника:
![]()
– на выходе:
![]() ,
, ![]() ;
; ![]() ,
,![]()
– начальные условия: при моменте![]() выполняются следующие условия:
выполняются следующие условия:![]() ,
, ![]() ,
,![]() ,
,
где ![]() – вектор скорости движения водной среды,
– вектор скорости движения водной среды,![]() – давление,
– давление, ![]() – коэффициент турбулентного обмена по горизонтальному направлению,
– коэффициент турбулентного обмена по горизонтальному направлению,![]() – коэффициент турбулентного обмена по вертикальному направлению,
– коэффициент турбулентного обмена по вертикальному направлению, ![]() – ускорение свободного падения,
– ускорение свободного падения,![]() – плотность жидкости,
– плотность жидкости,![]() – составляющая тангенциального напряжения (закон Ван-Дорна),
– составляющая тангенциального напряжения (закон Ван-Дорна), ![]() – плотность суспензии(взвеси). Система координат выбрана таким образом, что ось
– плотность суспензии(взвеси). Система координат выбрана таким образом, что ось![]() совмещена с дном водоема и направлена в сторону ледовой пластины, ось
совмещена с дном водоема и направлена в сторону ледовой пластины, ось![]() – вертикально вверх.
– вертикально вверх.
Имеются разные временные слои два реальных при![]() ,
,![]() и один промежуточный слой при
и один промежуточный слой при![]() соответственно можно обозначить
соответственно можно обозначить![]() ,
, ![]()
![]() ,
, ![]() .
.
Расщепляя уравнения (1), (2), по физическим процессам, получим:![]() , (6)
, (6) ![]() , (7)
, (7)
![]() ,
,![]() (8)
(8)
После дифференцирование по и уравнения (18), (18), (20) примут вид: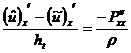 ,
,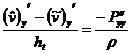 , (9)
, (9)
Суммируя уравнения (9), учитывая уравнение неразрывности (3)получим уравнение:![]() (10)
(10)
Расчет задач гидродинамики по данному методу осуществляется в три этапа. На первом этапе считается поле скоростей. На втором этапе рассчитывается давление. На третьем этапе уточняется поле скоростей по давлению.
Для аппроксимации задачи применяется интегро-интерполяционный метод, по области : ![]() :
: ![]() ,
,![]() :
: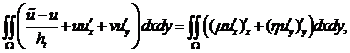
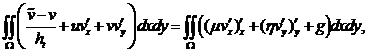
Уравнение (11) и (12) представляет собой конечно-разностную схему для уравнения (6) и (7).![]() (11)
(11)
аналогично:![]() (12)
(12)
.
Для аппроксимации операторов диффузии и конвекции по временной переменной будем использовать схемы с весами .
Также проинтегрируем уравнение (10) по области :![]() :
: ![]() :
: ![]() ,
, ![]() . (13)
. (13)
Тогда уравнение запишется в виде: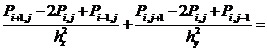
. 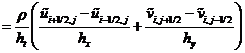 (14)
(14)
Проинтегрируем уравнение (9) по области : ![]() :
: ![]() :
:![]() , :
, :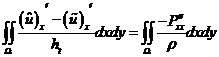 ,
, 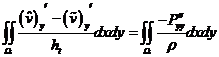 ,. (15)
,. (15)
. ![]() (16)
(16)
Аналогично можно записать конечно-разностную схему для уравнения:![]() , (17).
, (17).
Дискретная конечно-объемная модель волновой гидродинамики. Расчетные ячейки представляют собой прямоугольники, они могут быть заполненными, частично заполненными или пустыми. Центры ячеек и узлы разнесены на![]() , и
, и![]() по координатам
по координатам![]() и
и![]() соответственно. Обозначим через
соответственно. Обозначим через![]() заполненность ячейки
заполненность ячейки ![]() . Поле скоростей и давление рассчитываются в вершинах ячейки. Вершинами ячейки
. Поле скоростей и давление рассчитываются в вершинах ячейки. Вершинами ячейки![]() являются узлы
являются узлы![]() ,
,![]() ,
,![]() ,
,![]() .
.
Степень заполненности ячейки определяется давлением столба жидкости внутри данной ячейки. Если среднее давление в узлах, которые относятся к вершинам рассматриваемой ячейки, больше давления столба жидкости внутри ячейки, то ячейка считается заполненной полностью![]() . В общем случае заполненность ячейки можно вычислить по следующей формуле:
. В общем случае заполненность ячейки можно вычислить по следующей формуле:
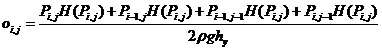 (18)
(18)
где 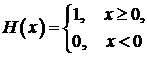 – функция Хевисайда.
– функция Хевисайда.
В окрестности узла![]() лежат ячейки
лежат ячейки![]() ,
,![]() ,
,![]() ,
,![]() .
.
Введутся коэффициенты![]()
![]() , ,
, ,![]() ,
,![]() ,
,![]() , описывающие заполненность областей, находящихся в окрестности ячейки. Значение
, описывающие заполненность областей, находящихся в окрестности ячейки. Значение![]() , характеризует заполненность всей области.
, характеризует заполненность всей области.
Заполненные части областей![]() будем называть
будем называть![]() , где
, где ![]() . В соответствии с этим коэффициенты
. В соответствии с этим коэффициенты![]() можно вычислить по формулам:
можно вычислить по формулам: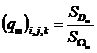 ,
,
а уравнение (11) примет вид:
![]()
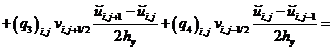
![]()
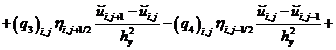
![]()
Также уравнение (12):
![]()
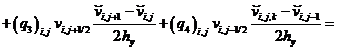
![]()
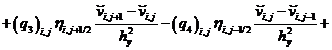 . (19)
. (19)
Далее представляется следующие сеточные уравнения:
– для составляющей вектора скорости![]() :
:![]()
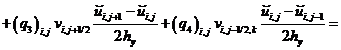
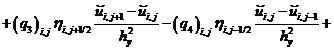
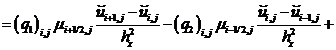 (20)
(20)
– для составляющей вектора скорости![]() :
:![]()
![]()
![]()
![]() ;
;
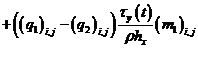 (21)
(21)
– сеточными уравнениями для расчета поля давления: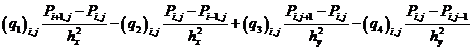 ;
;
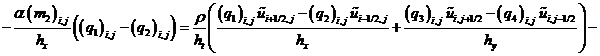
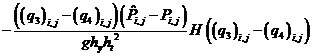 (22)
(22)
– уравнениями для уточнения поля скоростей по давлению: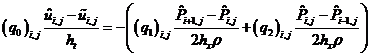 , (23)
, (23)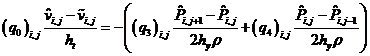 , (24)
, (24)
где параметр![]()
![]() , :. «маски» граничных условий.
, :. «маски» граничных условий.
Таким образом, построена конечно-объемная модель задачи волновой гидродинамики, представленная уравнениями (20) – (25).
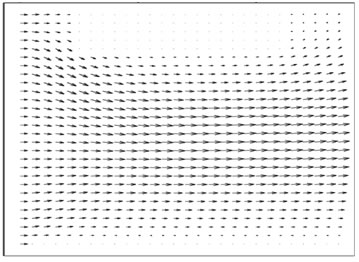
Рис.1. Поле вектора скоростей жидкости
Результаты численных экспериментов расчета движения водной среды, частично покрытой ледяной пластиной представлены на рис. 1, где изображена динамика набегающего к пластине потока воды.
Полученная модель, проектируемая для расчетной области с заданными численными значениями, являющимися размером сетки![]() с шагами по оси x и y соответствующимиhx, hy.
с шагами по оси x и y соответствующимиhx, hy.
Заключение. Разработана двумерная математическая модель для расчета полей скоростей; приведено описание программной реализации математической модели для расчета полей скоростей водной среды; выполнен численный эксперимент, построена картина потока воды водоема при наличии ледового покрытиявпериодов времени, которые согласуются с реальным физическим процессом.
Литература
1. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. М.: Физматлит, 2001. 320 с.
2. Стокер, Дж. Дж. Волны на воде. Пер. с англ. – М. : Иностр. литер., 1959. 618 с.